C++
Java
Python
Python3
C
C#
JavaScript
Ruby
Swift
Go
Scala
Kotlin
Rust
PHP
TypeScript
Racket
Erlang
Elixir
Dart
monokai
ambiance
chaos
chrome
cloud9_day
cloud9_night
cloud9_night_low_color
clouds
clouds_midnight
cobalt
crimson_editor
dawn
dracula
dreamweaver
eclipse
github
github_dark
gob
gruvbox
gruvbox_dark_hard
gruvbox_light_hard
idle_fingers
iplastic
katzenmilch
kr_theme
kuroir
merbivore
merbivore_soft
mono_industrial
nord_dark
one_dark
pastel_on_dark
solarized_dark
solarized_light
sqlserver
terminal
textmate
tomorrow
tomorrow_night
tomorrow_night_blue
tomorrow_night_bright
tomorrow_night_eighties
twilight
vibrant_ink
xcode
上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
}
};
运行代码
提交
java 解法, 执行用时: 0 ms, 内存消耗: 42.1 MB, 提交时间: 2024-10-27 17:15:56
class Solution {
public int[] findRedundantConnection(int[][] edges) {
int n = edges.length;
int[] parent = new int[n + 1];
for (int i = 1; i <= n; i++) {
parent[i] = i;
}
for (int i = 0; i < n; i++) {
int[] edge = edges[i];
int node1 = edge[0], node2 = edge[1];
if (find(parent, node1) != find(parent, node2)) {
union(parent, node1, node2);
} else {
return edge;
}
}
return new int[0];
}
public void union(int[] parent, int index1, int index2) {
parent[find(parent, index1)] = find(parent, index2);
}
public int find(int[] parent, int index) {
if (parent[index] != index) {
parent[index] = find(parent, parent[index]);
}
return parent[index];
}
}
javascript 解法, 执行用时: 11 ms, 内存消耗: 52.2 MB, 提交时间: 2024-10-27 17:14:46
/**
* @param {number[][]} edges
* @return {number[]}
*/
var findRedundantConnection = function(edges) {
const n = edges.length;
const parent = new Array(n + 1).fill(0).map((value, index) => index);
for (let i = 0; i < n; i++) {
const edge = edges[i];
const node1 = edge[0], node2 = edge[1];
if (find(parent, node1) != find(parent, node2)) {
union(parent, node1, node2);
} else {
return edge;
}
}
return [0];
};
const union = (parent, index1, index2) => {
parent[find(parent, index1)] = find(parent, index2);
}
const find = (parent, index) => {
if (parent[index] !== index) {
parent[index] = find(parent, parent[index]);
}
return parent[index];
}
golang 解法, 执行用时: 4 ms, 内存消耗: 2.9 MB, 提交时间: 2022-11-22 10:42:44
func findRedundantConnection(edges [][]int) []int {
parent := make([]int, len(edges)+1)
for i := range parent {
parent[i] = i
}
var find func(int) int
find = func(x int) int {
if parent[x] != x {
parent[x] = find(parent[x])
}
return parent[x]
}
union := func(from, to int) bool {
x, y := find(from), find(to)
if x == y {
return false
}
parent[x] = y
return true
}
for _, e := range edges {
if !union(e[0], e[1]) {
return e
}
}
return nil
}
python3 解法, 执行用时: 36 ms, 内存消耗: 15.3 MB, 提交时间: 2022-11-22 10:42:23
'''
并查集
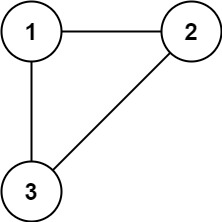
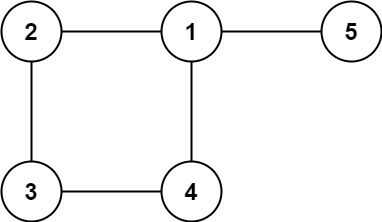
在一棵树中,边的数量比节点的数量少 1。如果一棵树有 n 个节点,则这棵树有 n−1 条边。
这道题中的图在树的基础上多了一条附加的边,因此边的数量也是 n。
树是一个连通且无环的无向图,在树中多了一条附加的边之后就会出现环,因此附加的边即为导致环出现的边。
可以通过并查集寻找附加的边。初始时,每个节点都属于不同的连通分量。
遍历每一条边,判断这条边连接的两个顶点是否属于相同的连通分量。
1.如果两个顶点属于不同的连通分量,则说明在遍历到当前的边之前,这两个顶点之间不连通,
因此当前的边不会导致环出现,合并这两个顶点的连通分量。
2.如果两个顶点属于相同的连通分量,则说明在遍历到当前的边之前,这两个顶点之间已经连通,
因此当前的边导致环出现,为附加的边,将当前的边作为答案返回。
'''
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
n = len(edges)
parent = list(range(n + 1))
def find(index: int) -> int:
if parent[index] != index:
parent[index] = find(parent[index])
return parent[index]
def union(index1: int, index2: int):
parent[find(index1)] = find(index2)
for node1, node2 in edges:
if find(node1) != find(node2):
union(node1, node2)
else:
return [node1, node2]
return []