蜡烛之间的盘子

2055. 蜡烛之间的盘子

给你一个长桌子，桌子上盘子和蜡烛排成一列。给你一个下标从 0 开始的字符串 s ，它只包含字符 '*' 和 '|' ，其中 '*' 表示一个盘子，'|' 表示一支蜡烛。

同时给你一个下标从 0 开始的二维整数数组 queries ，其中 queries[i] = [left_i, right_i] 表示 子字符串 s[left_i...right_i] （包含左右端点的字符）。对于每个查询，你需要找到 子字符串中 在 两支蜡烛之间 的盘子的数目。如果一个盘子在 子字符串中 左边和右边都至少有一支蜡烛，那么这个盘子满足在 两支蜡烛之间 。

比方说，s = "||**||**|*" ，查询 [3, 8] ，表示的是子字符串 "*||**|" 。子字符串中在两支蜡烛之间的盘子数目为 2 ，子字符串中右边两个盘子在它们左边和右边都至少有一支蜡烛。

请你返回一个整数数组 answer ，其中 answer[i] 是第 i 个查询的答案。

示例 1:

ex-1

输入：s = "**|**|***|", queries = [[2,5],[5,9]]
输出：[2,3]
解释：
- queries[0] 有两个盘子在蜡烛之间。
- queries[1] 有三个盘子在蜡烛之间。

示例 2:

ex-2

输入：s = "***|**|*****|**||**|*", queries = [[1,17],[4,5],[14,17],[5,11],[15,16]]
输出：[9,0,0,0,0]
解释：
- queries[0] 有 9 个盘子在蜡烛之间。
- 另一个查询没有盘子在蜡烛之间。

提示：

3 <= s.length <= 10⁵
s 只包含字符 '*' 和 '|' 。
1 <= queries.length <= 10⁵
queries[i].length == 2
0 <= left_i <= right_i < s.length

原站题解

去查看

上次编辑到这里，代码来自缓存点击恢复默认模板

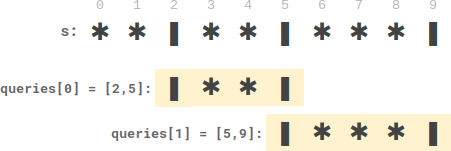
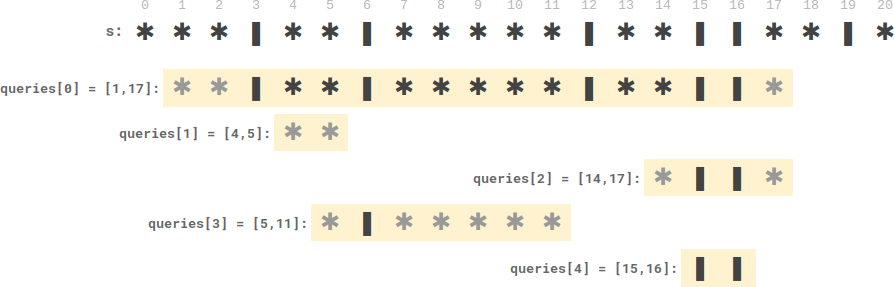
class Solution { public: vector<int> platesBetweenCandles(string s, vector<vector<int>>& queries) { } };

golang 解法, 执行用时: 248 ms, 内存消耗: 19.8 MB, 提交时间: 2023-06-12 09:45:12

func platesBetweenCandles(s string, queries [][]int) []int {
    n := len(s)
    presum, lefts, rights := make([]int, n + 1), make([]int, n), make([]int, n)
    for i, j, l, r := 0, n - 1, -1, -1; i < n; i++{
        if s[i] == '*' {
            presum[i + 1] = presum[i] + 1
        } else {
            presum[i + 1] = presum[i]
            l = i
        }
        if s[j] == '|' {
            r = j
        }
        lefts[i] = l
        rights[j] = r
        j--
    }
    ans := make([]int, len(queries))
    for i := 0; i < len(queries); i++ {
        if rights[queries[i][0]] >= 0 && lefts[queries[i][1]] >= 0 && lefts[queries[i][1]] > rights[queries[i][0]] {
            ans[i] = presum[lefts[queries[i][1]]] - presum[rights[queries[i][0]]]
        }
    }
    return ans
}

javascript 解法, 执行用时: 256 ms, 内存消耗: 75.1 MB, 提交时间: 2023-06-12 09:44:51

/**
 * @param {string} s
 * @param {number[][]} queries
 * @return {number[]}
 */
var platesBetweenCandles = function(s, queries) {
    const n = s.length
    const presum = new Array(n + 1).fill(0), lefts = new Array(n), rights = new Array(n)
    for(let i = 0, j = n - 1, l = -1, r = -1; i < n; i++, j--) {
        if(s.charAt(i) == '*')
            presum[i + 1] = presum[i] + 1
        else {
            presum[i + 1] = presum[i]
            l = i
        }
        if(s.charAt(j) == '|')
            r = j
        lefts[i] = l
        rights[j] = r
    }
    ans = new Array(queries.length).fill(0)
    for(let i = 0; i < queries.length; i++)
        if(lefts[queries[i][1]] >= 0 && rights[queries[i][0]] >= 0 && lefts[queries[i][1]] > rights[queries[i][0]])
            ans[i] = presum[lefts[queries[i][1]]] - presum[rights[queries[i][0]]]
    return ans
};

java 解法, 执行用时: 11 ms, 内存消耗: 75.1 MB, 提交时间: 2023-06-12 09:44:35

class Solution {
    public int[] platesBetweenCandles(String s, int[][] queries) {
        int n = s.length();
        int[] presum = new int[n + 1], lefts = new int[n], rights = new int[n];
        for(int i = 0, j = n - 1, l = -1, r = -1; i < n; i++, j--) {
            if(s.charAt(i) == '*')
                presum[i + 1] = presum[i] + 1;
            else {
                presum[i + 1] = presum[i];
                l = i;
            }
            if(s.charAt(j) == '|')
                r = j;
            lefts[i] = l;
            rights[j] = r;
        }
        int[] ans = new int[queries.length];
        for(int i = 0; i < queries.length; i++)
            if(lefts[queries[i][1]] >= 0 && rights[queries[i][0]] >= 0 && lefts[queries[i][1]] > rights[queries[i][0]])
                ans[i] = presum[lefts[queries[i][1]]] - presum[rights[queries[i][0]] + 1];
        return ans;
    }
}

python3 解法, 执行用时: 264 ms, 内存消耗: 46.7 MB, 提交时间: 2023-06-12 09:44:20

class Solution:
    def platesBetweenCandles(self, s: str, queries: List[List[int]]) -> List[int]:
        n = len(s)
        # presum: 统计*的前缀和, lefts: 统计每个坐标左边最近的|的坐标, rights: 统计每个坐标右边最近的|的坐标
        presum, lefts, rights, l = [0] * (n + 1), [-1] * n, [-1] * n, -1
        for i, c in enumerate(s):
            if c == '*':
                # 当前字符为*，前缀和个数加一
                presum[i + 1] = presum[i] + 1
            else:
                # 当前字符为|，前缀和个数不变
                presum[i + 1] = presum[i]
                # 更新最新的坐标最近坐标（接下来下次更新前最近的都是i）
                l = i
            lefts[i] = l
        # 右边与左边的更新同理，只需要从右往左
        r = -1
        for i, c in enumerate(s[::-1]):
            if c == '|':
                r = n - 1 - i
            rights[n - 1 - i] = r
        # 最终答案只有 左查询点的右边有蜡烛、右查询点的左边有蜡烛、且右边的蜡烛在左边的蜡烛右边中间才可能有*，否则肯定是0个
        return [presum[lefts[r]] - presum[rights[l]] if rights[l] >= 0 and lefts[r] >= 0 and rights[l] < lefts[r] else 0 for l, r in queries]

上一题

下一题

详情