上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
int maxSizeSlices(vector<int>& slices) {
}
};
javascript 解法, 执行用时: 72 ms, 内存消耗: 45.9 MB, 提交时间: 2023-08-18 07:48:33
/**
* @param {number[]} slices
* @return {number}
*/
var maxSizeSlices = function(slices) {
const v1 = slices.slice(1);
const v2 = slices.slice(0, slices.length - 1);
const ans1 = calculate(v1);
const ans2 = calculate(v2);
return Math.max(ans1, ans2);
};
const calculate = (slices) => {
const N = slices.length;
const n = Math.floor((slices.length + 1) / 3);
const dp = new Array(N).fill(0).map(() => new Array(n + 1).fill(-Infinity));
dp[0][0] = 0, dp[0][1] = slices[0];
dp[1][0] = 0, dp[1][1] = Math.max(slices[0], slices[1]);
for (let i = 2; i < N; i++) {
dp[i][0] = 0;
for (let j = 1; j <= n; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 2][j - 1] + slices[i]);
}
}
return dp[N - 1][n];
};
java 解法, 执行用时: 5 ms, 内存消耗: 41.9 MB, 提交时间: 2023-08-18 07:48:12
class Solution {
public int maxSizeSlices(int[] slices) {
int[] v1 = new int[slices.length - 1];
int[] v2 = new int[slices.length - 1];
System.arraycopy(slices, 1, v1, 0, slices.length - 1);
System.arraycopy(slices, 0, v2, 0, slices.length - 1);
int ans1 = calculate(v1);
int ans2 = calculate(v2);
return Math.max(ans1, ans2);
}
public int calculate(int[] slices) {
int N = slices.length, n = (N + 1) / 3;
int[][] dp = new int[N][n + 1];
for (int i = 0; i < N; i++) {
Arrays.fill(dp[i], Integer.MIN_VALUE);
}
dp[0][0] = 0;
dp[0][1] = slices[0];
dp[1][0] = 0;
dp[1][1] = Math.max(slices[0], slices[1]);
for (int i = 2; i < N; i++) {
dp[i][0] = 0;
for (int j = 1; j <= n; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 2][j - 1] + slices[i]);
}
}
return dp[N - 1][n];
}
}
golang 解法, 执行用时: 8 ms, 内存消耗: 6.5 MB, 提交时间: 2023-08-18 07:47:51
func max(a, b int) int {
if a > b {
return a
}
return b
}
func calculate(slices []int) int {
N, n := len(slices), (len(slices) + 1) / 3
dp := make([][]int, N)
for i := 0; i < N; i++ {
dp[i] = make([]int, n + 1)
for j := 0; j <= n; j++ {
dp[i][j] = -0x3f3f3f3f
}
}
dp[0][0], dp[0][1], dp[1][0], dp[1][1] = 0, slices[0], 0, max(slices[0], slices[1])
for i := 2; i < N; i++ {
dp[i][0] = 0
for j := 1; j <= n; j++ {
dp[i][j] = max(dp[i - 1][j], dp[i - 2][j - 1] + slices[i])
}
}
return dp[N - 1][n]
}
func maxSizeSlices(slices []int) int {
return max(calculate(slices[1:]), calculate(slices[:len(slices) - 1]))
}
python3 解法, 执行用时: 216 ms, 内存消耗: 17.4 MB, 提交时间: 2023-08-18 07:47:35
'''
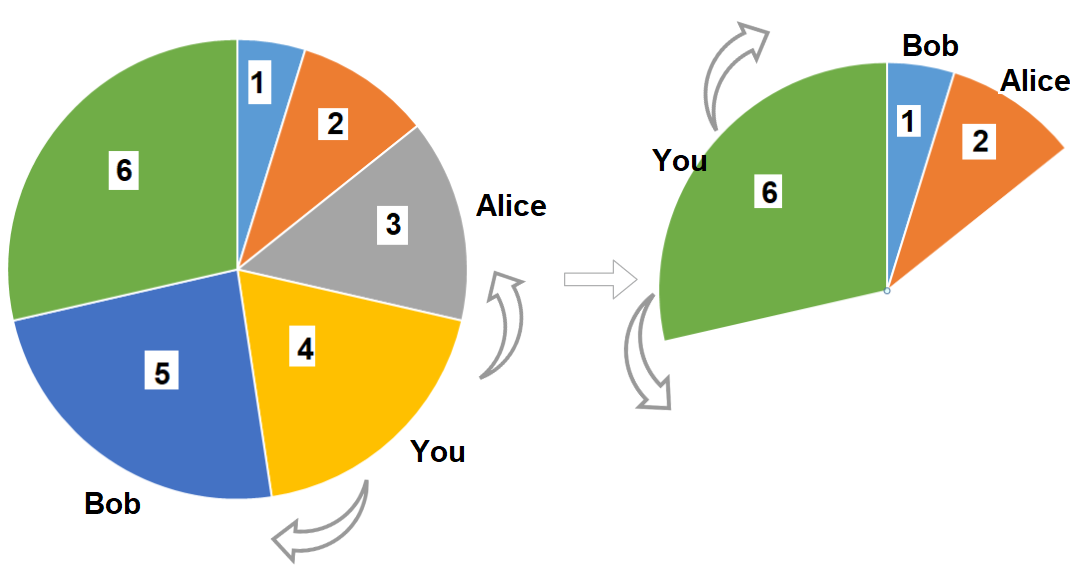
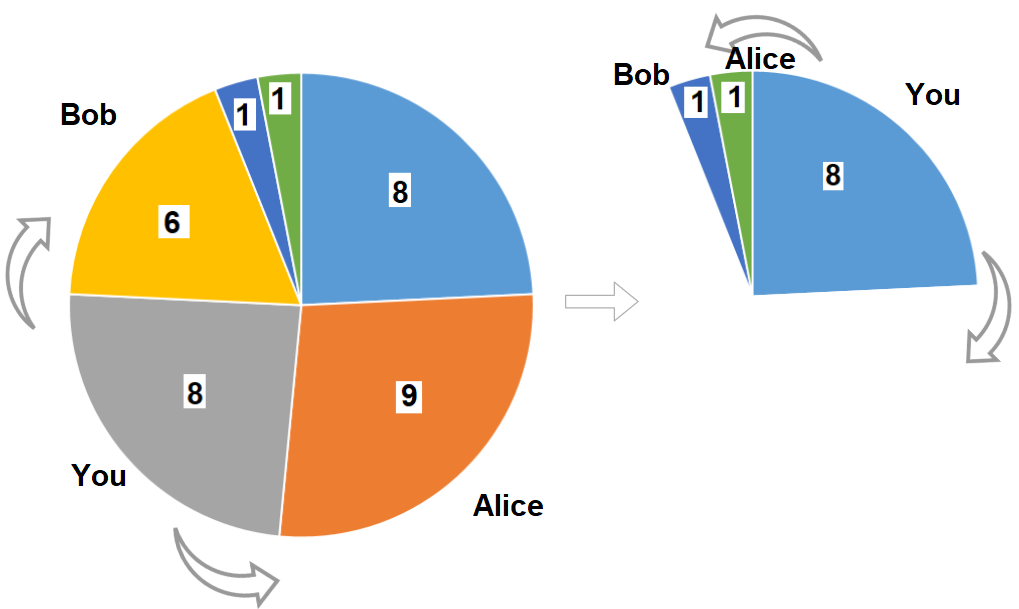
给一个长度为 3n 的环状序列,你可以在其中选择 n 个数,并且任意两个数不能相邻,求这 n 个数的最大值。
dp[i][j] 表示在前 i 个数中选择了 j 个不相邻的数的最大和:
'''
class Solution:
def maxSizeSlices(self, slices: List[int]) -> int:
def calculate(slices):
N, n = len(slices), (len(slices) + 1) // 3
dp = [[-10**9 for i in range(n + 1)] for j in range(N)]
dp[0][0], dp[0][1] = 0, slices[0]
dp[1][0], dp[1][1] = 0, max(slices[0], slices[1])
for i in range(2, N, 1):
dp[i][0] = 0
for j in range(1, n + 1, 1):
dp[i][j] = max(dp[i - 1][j], dp[i - 2][j - 1] + slices[i])
return dp[N - 1][n]
v1 = slices[1:]
v2 = slices[0:-1]
ans1 = calculate(v1)
ans2 = calculate(v2)
return max(ans1, ans2)