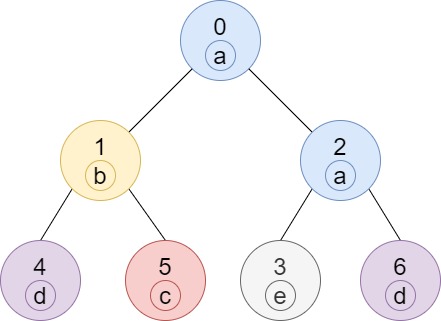
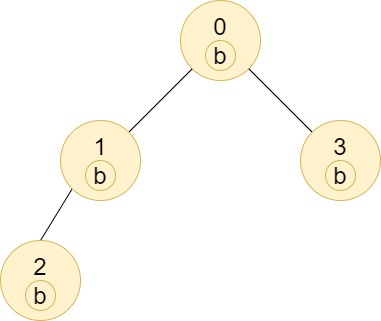
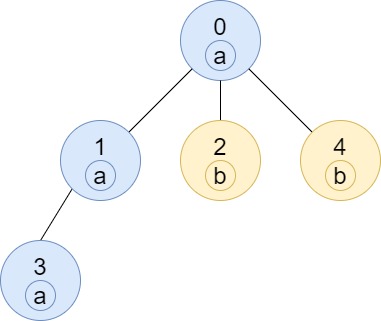
C++
Java
Python
Python3
C
C#
JavaScript
Ruby
Swift
Go
Scala
Kotlin
Rust
PHP
TypeScript
Racket
Erlang
Elixir
Dart
monokai
ambiance
chaos
chrome
cloud9_day
cloud9_night
cloud9_night_low_color
clouds
clouds_midnight
cobalt
crimson_editor
dawn
dracula
dreamweaver
eclipse
github
github_dark
gob
gruvbox
gruvbox_dark_hard
gruvbox_light_hard
idle_fingers
iplastic
katzenmilch
kr_theme
kuroir
merbivore
merbivore_soft
mono_industrial
nord_dark
one_dark
pastel_on_dark
solarized_dark
solarized_light
sqlserver
terminal
textmate
tomorrow
tomorrow_night
tomorrow_night_blue
tomorrow_night_bright
tomorrow_night_eighties
twilight
vibrant_ink
xcode
上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
vector<int> countSubTrees(int n, vector<vector<int>>& edges, string labels) {
}
};
运行代码
提交
java 解法, 执行用时: 47 ms, 内存消耗: 106.6 MB, 提交时间: 2023-09-23 11:04:39
class Solution {
public int[] countSubTrees(int n, int[][] edges, String labels) {
/*
后序遍历
*/
List<Integer>[] points = new List[n];
for(int i = 0; i < n; i++){
points[i] = new ArrayList<>();
}
for(int[] p : edges){
points[p[0]].add(p[1]);
points[p[1]].add(p[0]);
}
int[] ls = new int[n];
for(int i = 0; i < n; i++){
ls[i] = labels.charAt(i) - 'a';
}
res = new int[n];
visited = new boolean[n];
visited[0] = true;
dfs(0, points, ls);
return res;
}
int[] res;
boolean[] visited;
private int[] dfs(int i, List<Integer>[] points, int[] ls){
int[] curLs = new int[26];
//添加自身节点
curLs[ls[i]]++;
for(int child : points[i]){
/*
判断是否已经遍历过该节点,如果遍历过,那么跳过
因为这是无向图, 1 可以到 2,2 也可以到 1,因此,当 1 到 2 的时候,我们需要记录 1 已经访问
这样,从 2 出发,就不会再到 1 了
*/
if(visited[child]){
continue;
}
visited[child] = true;
int[] childLs = dfs(child, points, ls);
for(int k = 0; k < 26; k++){
curLs[k] += childLs[k];
}
}
res[i] = curLs[ls[i]];
return curLs;
}
}
python3 解法, 执行用时: 1208 ms, 内存消耗: 216.1 MB, 提交时间: 2023-09-23 11:02:26
class Solution:
def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:
g = collections.defaultdict(list)
for x, y in edges:
g[x].append(y)
g[y].append(x)
def dfs(o: int, pre: int):
f[o][ord(labels[o]) - ord("a")] = 1
for nex in g[o]:
if nex != pre:
dfs(nex, o)
for i in range(26):
f[o][i] += f[nex][i]
f = [[0] * 26 for _ in range(n)]
dfs(0, -1)
ans = [f[i][ord(labels[i]) - ord("a")] for i in range(n)]
return ans
cpp 解法, 执行用时: 672 ms, 内存消耗: 209.2 MB, 提交时间: 2023-09-23 11:02:01
class Solution {
public:
vector<vector<int>> g;
vector<vector<int>> f;
void dfs(int o, int pre, const string &labels) {
f[o][labels[o] - 'a'] = 1;
for (const auto &nex: g[o]) {
if (nex == pre) {
continue;
}
dfs(nex, o, labels);
for (int i = 0; i < 26; ++i) {
f[o][i] += f[nex][i];
}
}
}
vector<int> countSubTrees(int n, vector<vector<int>>& edges, string labels) {
g.resize(n);
for (const auto &edge: edges) {
g[edge[0]].push_back(edge[1]);
g[edge[1]].push_back(edge[0]);
}
f.assign(n, vector<int>(26));
dfs(0, -1, labels);
vector<int> ans;
for (int i = 0; i < n; ++i) {
ans.push_back(f[i][labels[i] - 'a']);
}
return ans;
}
};
golang 解法, 执行用时: 240 ms, 内存消耗: 46.4 MB, 提交时间: 2023-09-23 11:01:37
//1.建立节点间的关系邻接矩阵
//2.dfs递归计算每个节点子树(包含该节点)每个字母的计数,
// 通过传递父节点排除子节点到父节点的情况代替visited开销
//3.在递归,归到某个节点是记录下该节点所属字母的计算
func countSubTrees(n int, edges [][]int, labels string) []int {
relations := genRelations(edges)
ans := make([]int, n)
dfs(0, relations, labels, -1, &ans)
return ans
}
func dfs(i int, relations [][]int, labels string, visited int, ans *[]int) []int {
count := make([]int, 26)
count[labels[i] - 'a']++
for _, c := range relations[i] {
if c == visited {
continue
}
re := dfs(c, relations, labels, i, ans)
for i := 0; i < 26; i++ {
count[i] += re[i]
}
}
(*ans)[i] = count[labels[i]-'a']
return count
}
func genRelations(edges [][]int)[][]int {
relations := make([][]int, len(edges)+1)
for _, e := range edges {
relations[e[0]] = append(relations[e[0]], e[1])
relations[e[1]] = append(relations[e[1]], e[0])
}
return relations
}