树上最大得分和路径

6240. 树上最大得分和路径

一个 n 个节点的无向树，节点编号为 0 到 n - 1 ，树的根结点是 0 号节点。给你一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [a_i, b_i] ，表示节点 a_i 和 b_i 在树中有一条边。

在每一个节点 i 处有一扇门。同时给你一个都是偶数的数组 amount ，其中 amount[i] 表示：

如果 amount[i] 的值是负数，那么它表示打开节点 i 处门扣除的分数。
如果 amount[i] 的值是正数，那么它表示打开节点 i 处门加上的分数。

游戏按照如下规则进行：

一开始，Alice 在节点 0 处，Bob 在节点 bob 处。
每一秒钟，Alice 和 Bob 分别移动到相邻的节点。Alice 朝着某个 叶子结点 移动，Bob 朝着节点 0 移动。
对于他们之间路径上的 每一个 节点，Alice 和 Bob 要么打开门并扣分，要么打开门并加分。注意：
- 如果门 已经打开 （被另一个人打开），不会有额外加分也不会扣分。
- 如果 Alice 和 Bob 同时到达一个节点，他们会共享这个节点的加分或者扣分。换言之，如果打开这扇门扣 c 分，那么 Alice 和 Bob 分别扣 c / 2 分。如果这扇门的加分为 c ，那么他们分别加 c / 2 分。
如果 Alice 到达了一个叶子结点，她会停止移动。类似的，如果 Bob 到达了节点 0 ，他也会停止移动。注意这些事件互相独立，不会影响另一方移动。

请你返回 Alice 朝最优叶子结点移动的最大净得分。

示例 1：

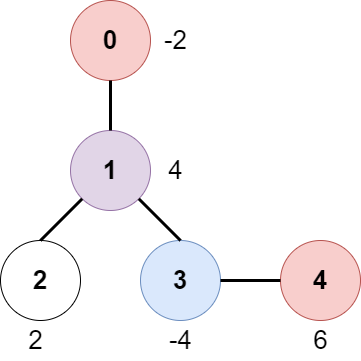
输入：edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6]
输出：6
解释：
上图展示了输入给出的一棵树。游戏进行如下：
- Alice 一开始在节点 0 处，Bob 在节点 3 处。他们分别打开所在节点的门。
  Alice 得分为 -2 。
- Alice 和 Bob 都移动到节点 1 。
  因为他们同时到达这个节点，他们一起打开门并平分得分。
  Alice 的得分变为 -2 + (4 / 2) = 0 。
- Alice 移动到节点 3 。因为 Bob 已经打开了这扇门，Alice 得分不变。
  Bob 移动到节点 0 ，并停止移动。
- Alice 移动到节点 4 并打开这个节点的门，她得分变为 0 + 6 = 6 。
现在，Alice 和 Bob 都不能进行任何移动了，所以游戏结束。
Alice 无法得到更高分数。

示例 2：

输入：edges = [[0,1]], bob = 1, amount = [-7280,2350]
输出：-7280
解释：
Alice 按照路径 0->1 移动，同时 Bob 按照路径 1->0 移动。
所以 Alice 只打开节点 0 处的门，她的得分为 -7280 。

提示：

2 <= n <= 10⁵
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
edges 表示一棵有效的树。
1 <= bob < n
amount.length == n
amount[i] 是范围 [-10⁴, 10⁴] 之间的一个偶数。

原站题解

去查看

上次编辑到这里，代码来自缓存点击恢复默认模板

class Solution { public: int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) { } };

golang 解法, 执行用时: 232 ms, 内存消耗: 42.3 MB, 提交时间: 2023-08-28 10:26:47

func mostProfitablePath(edges [][]int, bob int, amount []int) int {
	n := len(edges) + 1
	g := make([][]int, n)
	for _, e := range edges {
		x, y := e[0], e[1]
		g[x] = append(g[x], y)
		g[y] = append(g[y], x) // 建树
	}

	bobTime := make([]int, n) // bobTime[x] 表示 bob 访问节点 x 的时间
	for i := range bobTime {
		bobTime[i] = n // 也可以初始化成 inf
	}
	var dfsBob func(int, int, int) bool
	dfsBob = func(x, fa, t int) bool {
		if x == 0 {
			bobTime[x] = t
			return true
		}
		for _, y := range g[x] {
			if y != fa && dfsBob(y, x, t+1) {
				bobTime[x] = t // 只有可以到达 0 才标记访问时间
				return true
			}
		}
		return false
	}
	dfsBob(bob, -1, 0)

	g[0] = append(g[0], -1) // 防止把根节点当作叶子
	ans := math.MinInt32
	var dfsAlice func(int, int, int, int)
	dfsAlice = func(x, fa, aliceTime, sum int) {
		if aliceTime < bobTime[x] {
			sum += amount[x]
		} else if aliceTime == bobTime[x] {
			sum += amount[x] / 2
		}
		if len(g[x]) == 1 { // 叶子
			ans = max(ans, sum) // 更新答案
			return
		}
		for _, y := range g[x] {
			if y != fa {
				dfsAlice(y, x, aliceTime+1, sum)
			}
		}
	}
	dfsAlice(0, -1, 0, 0)
	return ans
}

func max(a, b int) int { if b > a { return b }; return a }

python3 解法, 执行用时: 456 ms, 内存消耗: 100.8 MB, 提交时间: 2023-08-28 10:26:29

class Solution:
    def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
        n = len(edges) + 1
        g = [[] for _ in range(n)]
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)  # 建树

        bob_time = [n] * n  # bobTime[x] 表示 bob 访问节点 x 的时间
        def dfs_bob(x: int, fa: int, t: int) -> bool:
            if x == 0:
                bob_time[x] = t
                return True
            for y in g[x]:
                if y != fa and dfs_bob(y, x, t + 1):
                    bob_time[x] = t  # 只有可以到达 0 才标记访问时间
                    return True
            return False
        dfs_bob(bob, -1, 0)

        g[0].append(-1)  # 防止把根节点当作叶子
        ans = -inf
        def dfs_alice(x: int, fa: int, alice_time: int, tot: int) -> None:
            if alice_time < bob_time[x]:
                tot += amount[x]
            elif alice_time == bob_time[x]:
                tot += amount[x] // 2
            if len(g[x]) == 1:  # 叶子
                nonlocal ans
                ans = max(ans, tot)  # 更新答案
                return
            for y in g[x]:
                if y != fa:
                    dfs_alice(y, x, alice_time + 1, tot)
        dfs_alice(0, -1, 0, 0)
        return ans

上一题

下一题

详情