出现频率最高的质数

100217. 出现频率最高的质数

给你一个大小为 m x n 、下标从 0 开始的二维矩阵 mat 。在每个单元格，你可以按以下方式生成数字：

最多有 8 条路径可以选择：东，东南，南，西南，西，西北，北，东北。
选择其中一条路径，沿着这个方向移动，并且将路径上的数字添加到正在形成的数字后面。
注意，每一步都会生成数字，例如，如果路径上的数字是 1, 9, 1，那么在这个方向上会生成三个数字：1, 19, 191 。

返回在遍历矩阵所创建的所有数字中，出现频率最高的、大于 10的质数；如果不存在这样的质数，则返回 -1 。如果存在多个出现频率最高的质数，那么返回其中最大的那个。

注意：移动过程中不允许改变方向。

示例 1：


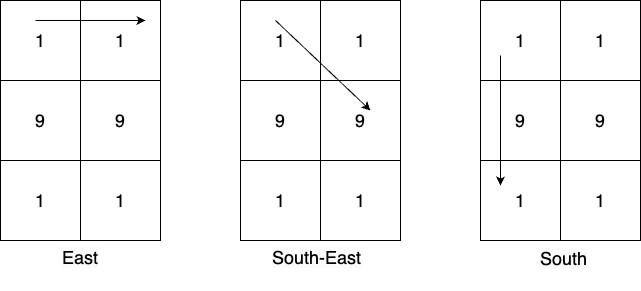
输入：mat = [[1,1],[9,9],[1,1]]
输出：19
解释： 
从单元格 (0,0) 出发，有 3 个可能的方向，这些方向上可以生成的大于 10 的数字有：
东方向: [11], 东南方向: [19], 南方向: [19,191] 。
从单元格 (0,1) 出发，所有可能方向上生成的大于 10 的数字有：[19,191,19,11] 。
从单元格 (1,0) 出发，所有可能方向上生成的大于 10 的数字有：[99,91,91,91,91] 。
从单元格 (1,1) 出发，所有可能方向上生成的大于 10 的数字有：[91,91,99,91,91] 。
从单元格 (2,0) 出发，所有可能方向上生成的大于 10 的数字有：[11,19,191,19] 。
从单元格 (2,1) 出发，所有可能方向上生成的大于 10 的数字有：[11,19,19,191] 。
在所有生成的数字中，出现频率最高的质数是 19 。

示例 2：

输入：mat = [[7]]
输出：-1
解释：唯一可以生成的数字是 7 。它是一个质数，但不大于 10 ，所以返回 -1 。

示例 3：

输入：mat = [[9,7,8],[4,6,5],[2,8,6]]
输出：97
解释： 
从单元格 (0,0) 出发，所有可能方向上生成的大于 10 的数字有: [97,978,96,966,94,942] 。
从单元格 (0,1) 出发，所有可能方向上生成的大于 10 的数字有: [78,75,76,768,74,79] 。
从单元格 (0,2) 出发，所有可能方向上生成的大于 10 的数字有: [85,856,86,862,87,879] 。
从单元格 (1,0) 出发，所有可能方向上生成的大于 10 的数字有: [46,465,48,42,49,47] 。
从单元格 (1,1) 出发，所有可能方向上生成的大于 10 的数字有: [65,66,68,62,64,69,67,68] 。
从单元格 (1,2) 出发，所有可能方向上生成的大于 10 的数字有: [56,58,56,564,57,58] 。
从单元格 (2,0) 出发，所有可能方向上生成的大于 10 的数字有: [28,286,24,249,26,268] 。
从单元格 (2,1) 出发，所有可能方向上生成的大于 10 的数字有: [86,82,84,86,867,85] 。
从单元格 (2,2) 出发，所有可能方向上生成的大于 10 的数字有: [68,682,66,669,65,658] 。
在所有生成的数字中，出现频率最高的质数是 97 。

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 6
1 <= mat[i][j] <= 9

原站题解

去查看

上次编辑到这里，代码来自缓存点击恢复默认模板

class Solution { public: int mostFrequentPrime(vector<vector<int>>& mat) { } };

golang 解法, 执行用时: 11 ms, 内存消耗: 3 MB, 提交时间: 2024-02-19 11:40:33

func isPrime(n int) bool {
	for i := 2; i*i <= n; i++ {
		if n%i == 0 {
			return false
		}
	}
	return true
}

func mostFrequentPrime(mat [][]int) int {
	dirs := []struct{ x, y int }{{1, 0}, {1, 1}, {0, 1}, {-1, 1}, {-1, 0}, {-1, -1}, {0, -1}, {1, -1}}
	m, n := len(mat), len(mat[0])
	cnt := map[int]int{}
	for i, row := range mat {
		for j, v := range row {
			for _, d := range dirs {
				x, y, v := i+d.x, j+d.y, v
				for 0 <= x && x < m && 0 <= y && y < n {
					v = v*10 + mat[x][y]
					// 如果 v 在 cnt 中，那么 v 一定是质数
					if cnt[v] > 0 || isPrime(v) {
						cnt[v]++
					}
					x += d.x
					y += d.y
				}
			}
		}
	}

	ans, maxCnt := -1, 0
	for v, c := range cnt {
		if c > maxCnt {
			ans, maxCnt = v, c
		} else if c == maxCnt {
			ans = max(ans, v)
		}
	}
	return ans
}

python3 解法, 执行用时: 132 ms, 内存消耗: 16.5 MB, 提交时间: 2024-02-19 11:37:55

# 每个单元格， 枚举8个方向，生成数字，统计其中质数个数
class Solution:
    def mostFrequentPrime(self, mat: List[List[int]]) -> int:
        m, n = len(mat), len(mat[0])
        cnt = Counter()
        for i, row in enumerate(mat):
            for j, v in enumerate(row):
                for dx, dy in (1, 0), (1, 1), (0, 1), (-1, 1), (-1, 0), (-1, -1), (0, -1), (1, -1):
                    x, y, val = i + dx, j + dy, v
                    while 0 <= x < m and 0 <= y < n:
                        val = val * 10 + mat[x][y]
                        # 如果 val 在 cnt 中，那么 val 一定是质数
                        if val in cnt or self.is_prime(val):
                            cnt[val] += 1
                        x += dx
                        y += dy

        ans, max_cnt = -1, 0
        for v, c in cnt.items():
            if c > max_cnt:
                ans, max_cnt = v, c
            elif c == max_cnt:
                ans = max(ans, v)
        return ans

    def is_prime(self, n: int) -> bool:
        return all(n % i for i in range(2, isqrt(n) + 1))

上一题

下一题

详情