class Solution {
public:
int minimumOperations(vector<vector<int>>& grid) {
}
};
2123. 使矩阵中的 1 互不相邻的最小操作数
给你一个 下标从 0 开始 的矩阵 grid。每次操作,你可以把 grid 中的 一个 1 变成 0 。
如果一个矩阵中,没有 1 与其它的 1 四连通(也就是说所有 1 在上下左右四个方向上不能与其他 1 相邻),那么该矩阵就是 完全独立 的。
请返回让 grid 成为 完全独立 的矩阵的 最小操作数。
示例 1:
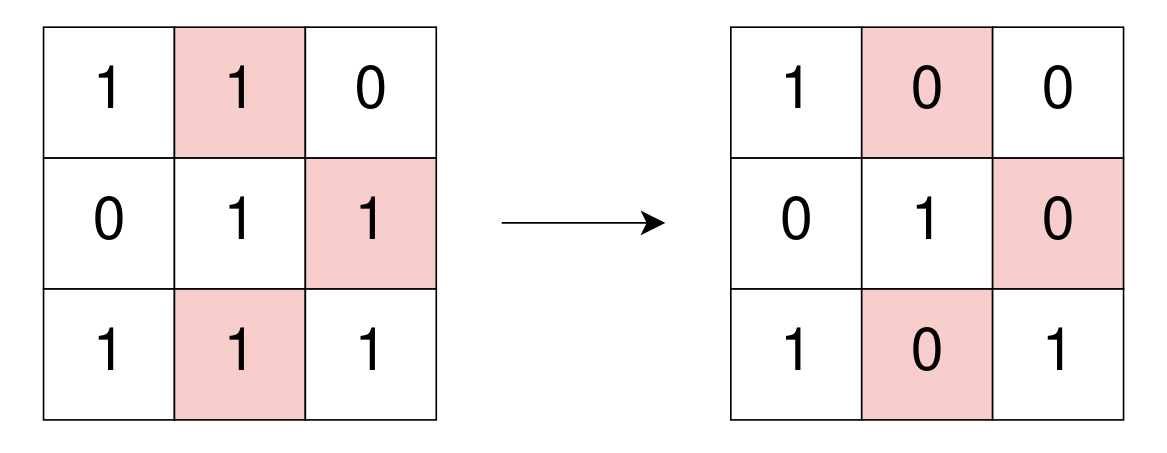
输入: grid = [[1,1,0],[0,1,1],[1,1,1]] 输出: 3 解释: 可以进行三次操作(把 grid[0][1], grid[1][2] 和 grid[2][1] 变成 0)。 操作后的矩阵中的所有的 1 与其它 1 均不相邻,因此矩阵是完全独立的。
示例 2:
输入: grid = [[0,0,0],[0,0,0],[0,0,0]] 输出: 0 解释: 矩阵中没有 1,此时矩阵也是完全独立的,因此无需操作,返回 0。
示例 3:
输入: grid = [[0,1],[1,0]] 输出: 0 解释: 矩阵中的所有的 1 与其它 1 均不相邻,已经是完全独立的,因此无需操作,返回 0。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]是0或者1.
原站题解