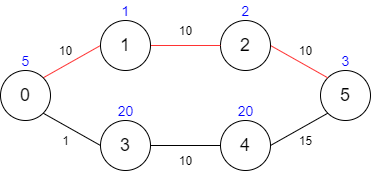
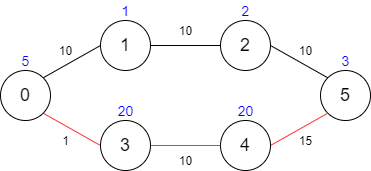
C++
Java
Python
Python3
C
C#
JavaScript
Ruby
Swift
Go
Scala
Kotlin
Rust
PHP
TypeScript
Racket
Erlang
Elixir
Dart
monokai
ambiance
chaos
chrome
cloud9_day
cloud9_night
cloud9_night_low_color
clouds
clouds_midnight
cobalt
crimson_editor
dawn
dracula
dreamweaver
eclipse
github
github_dark
gob
gruvbox
gruvbox_dark_hard
gruvbox_light_hard
idle_fingers
iplastic
katzenmilch
kr_theme
kuroir
merbivore
merbivore_soft
mono_industrial
nord_dark
one_dark
pastel_on_dark
solarized_dark
solarized_light
sqlserver
terminal
textmate
tomorrow
tomorrow_night
tomorrow_night_blue
tomorrow_night_bright
tomorrow_night_eighties
twilight
vibrant_ink
xcode
上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {
}
};
运行代码
提交
rust 解法, 执行用时: 79 ms, 内存消耗: 5.9 MB, 提交时间: 2024-10-03 08:54:46
use std::cmp::min;
impl Solution {
pub fn min_cost(max_time: i32, edges: Vec<Vec<i32>>, passing_fees: Vec<i32>) -> i32 {
let n = passing_fees.len();
let mut f = vec![vec![i32::MAX; n]; (max_time + 1) as usize];
f[0][0] = passing_fees[0];
for t in 1..=max_time {
for edge in &edges {
let (i, j, cost) = (edge[0] as usize, edge[1] as usize, edge[2]);
if cost <= t {
if f[(t - cost) as usize][j] != i32::MAX {
f[t as usize][i] = min(f[t as usize][i], f[(t - cost) as usize][j] + passing_fees[i]);
}
if f[(t - cost) as usize][i] != i32::MAX {
f[t as usize][j] = min(f[t as usize][j], f[(t - cost) as usize][i] + passing_fees[j]);
}
}
}
}
let mut ans = i32::MAX;
for t in 1..=max_time {
ans = min(ans, f[t as usize][n - 1]);
}
if ans == i32::MAX {
-1
} else {
ans
}
}
}
javascript 解法, 执行用时: 497 ms, 内存消耗: 76.5 MB, 提交时间: 2024-10-03 08:54:02
/**
* @param {number} maxTime
* @param {number[][]} edges
* @param {number[]} passingFees
* @return {number}
*/
var minCost = function(maxTime, edges, passingFees) {
const n = passingFees.length;
const f = Array.from({ length: maxTime + 1 }, () => Array(n).fill(Infinity));
f[0][0] = passingFees[0];
for (let t = 1; t <= maxTime; t++) {
for (const [i, j, cost] of edges) {
if (cost <= t) {
if (f[t - cost][j] !== Infinity) {
f[t][i] = Math.min(f[t][i], f[t - cost][j] + passingFees[i]);
}
if (f[t - cost][i] !== Infinity) {
f[t][j] = Math.min(f[t][j], f[t - cost][i] + passingFees[j]);
}
}
}
}
let ans = Infinity;
for (let t = 1; t <= maxTime; t++) {
ans = Math.min(ans, f[t][n - 1]);
}
return ans === Infinity ? -1 : ans;
};
golang 解法, 执行用时: 40 ms, 内存消耗: 7.1 MB, 提交时间: 2023-10-27 22:17:07
var minFee = 10000000
var vis []bool
var lastVisTime []int
var lastVisFee []int
type pairs struct {
city, time, fee int
}
func minCost(maxTime int, edges [][]int, passingFees []int) int {
minFee = 10000000
prs := make([][]pairs, len(passingFees)) // 邻接表
vis = make([]bool, len(passingFees))
vis[0] = true
lastVisTime = make([]int, len(passingFees))
lastVisFee = make([]int, len(passingFees))
for i := range lastVisFee {
lastVisFee[i] = math.MaxInt32
lastVisTime[i] = math.MaxInt32
}
for _, e := range edges {
prs[e[0]] = append(prs[e[0]], pairs{
city: e[1],
time: e[2],
fee: passingFees[e[1]],
})
prs[e[1]] = append(prs[e[1]], pairs{
city: e[0],
time: e[2],
fee: passingFees[e[0]],
})
}
dfs(maxTime, prs, 0, passingFees[0], 0)
if minFee == 10000000 {
return -1
}
return minFee
}
func dfs(maxTime int, prs [][]pairs, curCity int, curFee, curTime int) {
if curTime > maxTime || curFee >= minFee{
return
}
if curFee > lastVisFee[curCity] && curTime > lastVisTime[curCity] {
return
}
lastVisFee[curCity] = min(lastVisFee[curCity], curFee)
lastVisTime[curCity] = min(lastVisTime[curCity], curTime)
if curCity == len(prs) - 1 {
minFee = curFee
return
}
for _, nx := range prs[curCity] {
if !vis[nx.city] {
vis[nx.city] = true
dfs(maxTime, prs, nx.city, curFee + nx.fee, curTime + nx.time)
vis[nx.city] = false
}
}
}
func min(i,j int) int {
if i < j {
return i
}
return j
}
java 解法, 执行用时: 90 ms, 内存消耗: 54 MB, 提交时间: 2023-10-27 22:16:27
import java.util.Arrays;
class Solution {
public int minCost(int maxTime, int[][] edges, int[] passingFees) {
int n=passingFees.length;
int INF=Integer.MAX_VALUE/2;
int[][]dp=new int[maxTime+1][n];
for(int i=0;i<dp.length;i++) Arrays.fill(dp[i],INF);
//初始化 对动态规划的状态定义dp[i][j] i是花费的时间 j是所到达的城市
dp[0][0]=passingFees[0];
//
int res=INF;
for(int t=1;t<=maxTime;t++){
for(int i=0;i<edges.length;i++){
int[]v=edges[i];
int x=v[0];//x->y
int y=v[1];//y->X
int cost=v[2];
if(cost<=t){
dp[t][y]=Math.min(dp[t][y],dp[t-cost][x]+passingFees[y]);
dp[t][x]=Math.min(dp[t][x],dp[t-cost][y]+passingFees[x]);
}
}
res=Math.min(res,dp[t][n-1]);
}
return res==INF?-1:res;
}
}
python3 解法, 执行用时: 7276 ms, 内存消耗: 39.1 MB, 提交时间: 2023-10-27 22:15:59
class Solution:
def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:
n = len(passingFees)
# f[t][i] 表示使用恰好 t 分钟到达城市 i 需要的最少通行费总和。
f = [[float("inf")] * n for _ in range(maxTime + 1)]
f[0][0] = passingFees[0]
for t in range(1, maxTime + 1):
for i, j, cost in edges:
if cost <= t:
f[t][i] = min(f[t][i], f[t - cost][j] + passingFees[i])
f[t][j] = min(f[t][j], f[t - cost][i] + passingFees[j])
ans = min(f[t][n - 1] for t in range(1, maxTime + 1))
return -1 if ans == float("inf") else ans
cpp 解法, 执行用时: 740 ms, 内存消耗: 91.3 MB, 提交时间: 2023-10-27 22:15:25
class Solution {
private:
// 极大值
static constexpr int INFTY = INT_MAX / 2;
public:
int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {
int n = passingFees.size();
vector<vector<int>> f(maxTime + 1, vector<int>(n, INFTY));
f[0][0] = passingFees[0];
for (int t = 1; t <= maxTime; ++t) {
for (const auto& edge: edges) {
int i = edge[0], j = edge[1], cost = edge[2];
if (cost <= t) {
f[t][i] = min(f[t][i], f[t - cost][j] + passingFees[i]);
f[t][j] = min(f[t][j], f[t - cost][i] + passingFees[j]);
}
}
}
int ans = INFTY;
for (int t = 1; t <= maxTime; ++t) {
ans = min(ans, f[t][n - 1]);
}
return ans == INFTY ? -1 : ans;
}
};