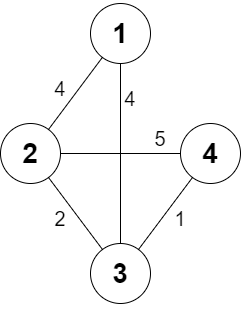
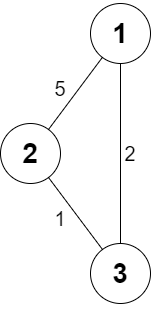
C++
Java
Python
Python3
C
C#
JavaScript
TypeScript
PHP
Swift
Kotlin
Dart
Go
Ruby
Scala
Rust
Racket
Erlang
Elixir
monokai
ambiance
chaos
chrome
cloud9_day
cloud9_night
cloud9_night_low_color
clouds
clouds_midnight
cobalt
crimson_editor
dawn
dracula
dreamweaver
eclipse
github
github_dark
gob
gruvbox
gruvbox_dark_hard
gruvbox_light_hard
idle_fingers
iplastic
katzenmilch
kr_theme
kuroir
merbivore
merbivore_soft
mono_industrial
nord_dark
one_dark
pastel_on_dark
solarized_dark
solarized_light
sqlserver
terminal
textmate
tomorrow
tomorrow_night
tomorrow_night_blue
tomorrow_night_bright
tomorrow_night_eighties
twilight
vibrant_ink
xcode
上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
vector<long long> minCost(int n, vector<vector<int>>& roads, vector<int>& appleCost, int k) {
}
};
运行代码
提交
java 解法, 执行用时: 2117 ms, 内存消耗: 43.7 MB, 提交时间: 2023-10-22 10:46:28
class Solution {
class Test{
Integer nextRoad;
Integer cost;
Test(int nextRoad,int cost){
this.nextRoad = nextRoad;
this.cost = cost;
}
}
class Road{
Integer road;
Integer cost;
List<Integer> list = new ArrayList<>();
Road(int road,int cost){
this.road = road;
this.cost = cost;
}
}
public long[] minCost(int n, int[][] roads, int[] appleCost, int k) {
Map<Integer,List<Test>> map = new HashMap<>();
for(int [] road : roads){
if(map.containsKey(road[0])){
Test test = new Test(road[1],road[2]);
map.get(road[0]).add(test);
}else {
List<Test> tests = new ArrayList<>();
tests.add(new Test(road[1],road[2]));
map.put(road[0],tests);
}
if(map.containsKey(road[1])){
Test test = new Test(road[0],road[2]);
map.get(road[1]).add(test);
}else {
List<Test> tests = new ArrayList<>();
tests.add(new Test(road[0],road[2]));
map.put(road[1],tests);
}
}
long[] ret = new long[n];
for(int i = 1; i <= n ; i ++){
int min = appleCost[i - 1];
Deque<Road> roadsDeque = new LinkedList<>();
Road road1 = new Road(i,0);
road1.list.add(i);
roadsDeque.add(road1);
while (!roadsDeque.isEmpty()){
Road road = roadsDeque.pollFirst();
List<Test> tests = map.get(road.road);
if(tests == null)
break;
for(Test test : tests){
int next = test.nextRoad;
int cost = test.cost;
if(road.list.contains(next) || road.cost > min)
continue;
int temp = appleCost[next - 1] + cost + k*cost + road.cost;
min = Math.min(temp,min);
Road road2 = new Road(next,cost+ k*cost + road.cost);
road2.list.addAll(road.list);
road2.list.add(next);
roadsDeque.add(road2);
}
}
ret[i - 1] = min;
}
//广度优先遍历
return ret;
}
}
python3 解法, 执行用时: 1096 ms, 内存消耗: 17 MB, 提交时间: 2023-10-22 10:45:57
class Solution:
def minCost(self, n: int, roads: List[List[int]], appleCost: List[int], k: int) -> List[int]:
g = defaultdict(list)
for a, b, cost in roads:
g[a - 1].append([b - 1, cost])
g[b - 1].append([a - 1, cost])
def dijkstra(start: int):
ans = float('inf')
dist = [float('inf')] * n
dist[start] = 0
q = [(0, start)]
while q:
cost, x = heapq.heappop(q)
ans = min(ans, cost * (k + 1) + appleCost[x])
if dist[x] < cost:
continue
for y, cost in g[x]:
d = dist[x] + cost
if d < dist[y]:
dist[y] = d
heapq.heappush(q, (d, y))
return ans
ans = [0] * n
for i in range(n):
ans[i] = dijkstra(i)
return ans
python3 解法, 执行用时: 56 ms, 内存消耗: 17 MB, 提交时间: 2023-10-22 10:45:39
class Solution:
def minCost(self, n: int, roads: List[List[int]], appleCost: List[int], k: int) -> List[int]:
g = collections.defaultdict(list)
for a, b, c in roads:
g[a - 1].append((b - 1, c * (k + 1)))
g[b - 1].append((a - 1, c * (k + 1)))
visit = [0] * n
pq = sorted((c, i) for i, c in enumerate(appleCost))
while pq:
c, u = heapq.heappop(pq)
if visit[u]:
continue
visit[u] = 1
for v, nc in g[u]:
if appleCost[v] > c + nc:
appleCost[v] = c + nc
heapq.heappush(pq, (appleCost[v], v))
return appleCost
cpp 解法, 执行用时: 12 ms, 内存消耗: 11.7 MB, 提交时间: 2023-10-22 10:45:24
typedef pair<int, int> PII;
const int N = 1010;
bool st[N];
int e[N << 1], w[N << 1], ne[N << 1], h[N], idx;
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
class Solution {
public:
vector<long long> minCost(int n, vector<vector<int>>& roads, vector<int>& appleCost, int k) {
memset(st, false, sizeof(st));
memset(h, -1, sizeof(h)), idx = 0;
for (auto& road : roads) {
int a = road[0] - 1, b = road[1] - 1, c = road[2];
add(a, b, c * (k + 1)), add(b, a, c * (k + 1));
}
priority_queue<PII, vector<PII>, greater<PII>> pq;
for (int i = 0; i < n; ++i) pq.emplace(appleCost[i], i);
while (!pq.empty()) {
auto [c, u] = pq.top();
pq.pop();
if (st[u]) continue;
st[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (appleCost[v] > c + w[i]) {
appleCost[v] = c + w[i];
pq.emplace(appleCost[v], v);
}
}
}
return vector<long long>(appleCost.begin(), appleCost.end());
}
};