上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
int minCostConnectPoints(vector<vector<int>>& points) {
}
};
python3 解法, 执行用时: 152 ms, 内存消耗: 16.1 MB, 提交时间: 2022-11-27 11:37:11
class DisjointSetUnion:
def __init__(self, n):
self.n = n
self.rank = [1] * n
self.f = list(range(n))
def find(self, x: int) -> int:
if self.f[x] == x:
return x
self.f[x] = self.find(self.f[x])
return self.f[x]
def unionSet(self, x: int, y: int) -> bool:
fx, fy = self.find(x), self.find(y)
if fx == fy:
return False
if self.rank[fx] < self.rank[fy]:
fx, fy = fy, fx
self.rank[fx] += self.rank[fy]
self.f[fy] = fx
return True
class BIT:
def __init__(self, n):
self.n = n
self.tree = [float("inf")] * n
self.idRec = [-1] * n
self.lowbit = lambda x: x & (-x)
def update(self, pos: int, val: int, identity: int):
while pos > 0:
if self.tree[pos] > val:
self.tree[pos] = val
self.idRec[pos] = identity
pos -= self.lowbit(pos)
def query(self, pos: int) -> int:
minval, j = float("inf"), -1
while pos < self.n:
if minval > self.tree[pos]:
minval = self.tree[pos]
j = self.idRec[pos]
pos += self.lowbit(pos)
return j
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
n = len(points)
edges = list()
def build(pos: List[Tuple[int, int, int]]):
pos.sort()
a = [y - x for (x, y, _) in pos]
b = sorted(set(a))
num = len(b)
bit = BIT(num + 1)
for i in range(n - 1, -1, -1):
poss = bisect.bisect(b, a[i])
j = bit.query(poss)
if j != -1:
dis = abs(pos[i][0] - pos[j][0]) + abs(pos[i][1] - pos[j][1])
edges.append((dis, pos[i][2], pos[j][2]))
bit.update(poss, pos[i][0] + pos[i][1], i)
def solve():
pos = [(x, y, i) for i, (x, y) in enumerate(points)]
build(pos)
pos = [(y, x, i) for i, (x, y) in enumerate(points)]
build(pos)
pos = [(-y, x, i) for i, (x, y) in enumerate(points)]
build(pos)
pos = [(x, -y, i) for i, (x, y) in enumerate(points)]
build(pos)
solve()
dsu = DisjointSetUnion(n)
edges.sort()
ret, num = 0, 1
for length, x, y in edges:
if dsu.unionSet(x, y):
ret += length
num += 1
if num == n:
break
return ret
golang 解法, 执行用时: 12 ms, 内存消耗: 6.4 MB, 提交时间: 2022-11-27 11:36:56
type unionFind struct {
parent, rank []int
}
func newUnionFind(n int) *unionFind {
parent := make([]int, n)
rank := make([]int, n)
for i := range parent {
parent[i] = i
rank[i] = 1
}
return &unionFind{parent, rank}
}
func (uf *unionFind) find(x int) int {
if uf.parent[x] != x {
uf.parent[x] = uf.find(uf.parent[x])
}
return uf.parent[x]
}
func (uf *unionFind) union(x, y int) bool {
fx, fy := uf.find(x), uf.find(y)
if fx == fy {
return false
}
if uf.rank[fx] < uf.rank[fy] {
fx, fy = fy, fx
}
uf.rank[fx] += uf.rank[fy]
uf.parent[fy] = fx
return true
}
type fenwickTree struct {
tree, idRec []int
}
func newFenwickTree(n int) *fenwickTree {
tree := make([]int, n)
idRec := make([]int, n)
for i := range tree {
tree[i], idRec[i] = math.MaxInt64, -1
}
return &fenwickTree{tree, idRec}
}
func (f *fenwickTree) update(pos, val, id int) {
for ; pos > 0; pos &= pos - 1 {
if val < f.tree[pos] {
f.tree[pos], f.idRec[pos] = val, id
}
}
}
func (f *fenwickTree) query(pos int) int {
minVal, minID := math.MaxInt64, -1
for ; pos < len(f.tree); pos += pos & -pos {
if f.tree[pos] < minVal {
minVal, minID = f.tree[pos], f.idRec[pos]
}
}
return minID
}
func dist(p, q []int) int {
return abs(p[0]-q[0]) + abs(p[1]-q[1])
}
func minCostConnectPoints(points [][]int) (ans int) {
n := len(points)
for i, p := range points {
points[i] = append(p, i)
}
type edge struct{ v, w, dis int }
edges := []edge{}
build := func() {
sort.Slice(points, func(i, j int) bool { a, b := points[i], points[j]; return a[0] < b[0] || a[0] == b[0] && a[1] < b[1] })
// 离散化 y-x
type pair struct{ v, i int }
ps := make([]pair, n)
for i, p := range points {
ps[i] = pair{p[1] - p[0], i}
}
sort.Slice(ps, func(i, j int) bool { return ps[i].v < ps[j].v })
kth := make([]int, n)
k := 1
kth[ps[0].i] = k
for i := 1; i < n; i++ {
if ps[i].v != ps[i-1].v {
k++
}
kth[ps[i].i] = k
}
t := newFenwickTree(k + 1)
for i := n - 1; i >= 0; i-- {
p := points[i]
pos := kth[i]
if j := t.query(pos); j != -1 {
q := points[j]
edges = append(edges, edge{p[2], q[2], dist(p, q)})
}
t.update(pos, p[0]+p[1], i)
}
}
build()
for _, p := range points {
p[0], p[1] = p[1], p[0]
}
build()
for _, p := range points {
p[0] = -p[0]
}
build()
for _, p := range points {
p[0], p[1] = p[1], p[0]
}
build()
sort.Slice(edges, func(i, j int) bool { return edges[i].dis < edges[j].dis })
uf := newUnionFind(n)
left := n - 1
for _, e := range edges {
if uf.union(e.v, e.w) {
ans += e.dis
left--
if left == 0 {
break
}
}
}
return
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
javascript 解法, 执行用时: 1212 ms, 内存消耗: 98.2 MB, 提交时间: 2022-11-27 11:36:31
/**
* @param {number[][]} points
* @return {number}
*/
var minCostConnectPoints = function(points) {
const dist = (x, y) => {
return Math.abs(points[x][0] - points[y][0]) + Math.abs(points[x][1] - points[y][1]);
}
const n = points.length;
const dsu = new DisjointSetUnion(n);
const edges = [];
for (let i = 0; i < n; i++) {
for (let j = i + 1; j < n; j++) {
edges.push([dist(i, j), i, j]);
}
}
edges.sort((a, b) => a[0] - b[0]);
let ret = 0, num = 1;
for (const [length, x, y] of edges) {
if (dsu.unionSet(x, y)) {
ret += length;
num += 1;
if (num === n) {
break;
}
}
}
return ret;
};
class DisjointSetUnion {
constructor(n) {
this.n = n;
this.rank = new Array(n).fill(1);
this.f = new Array(n).fill(0).map((element, index) => index);
}
find(x) {
if (this.f[x] === x) {
return x;
}
this.f[x] = this.find(this.f[x]);
return this.f[x];
}
unionSet(x, y) {
let fx = this.find(x), fy = this.find(y);
if (fx === fy) {
return false;
}
if (this.rank[fx] < this.rank[fy]) {
[fx, fy] = [fy, fx];
}
this.rank[fx] += this.rank[fy];
this.f[fy] = fx;
return true;
}
}
golang 解法, 执行用时: 304 ms, 内存消耗: 30.1 MB, 提交时间: 2022-11-27 11:36:15
type unionFind struct {
parent, rank []int
}
func newUnionFind(n int) *unionFind {
parent := make([]int, n)
rank := make([]int, n)
for i := range parent {
parent[i] = i
rank[i] = 1
}
return &unionFind{parent, rank}
}
func (uf *unionFind) find(x int) int {
if uf.parent[x] != x {
uf.parent[x] = uf.find(uf.parent[x])
}
return uf.parent[x]
}
func (uf *unionFind) union(x, y int) bool {
fx, fy := uf.find(x), uf.find(y)
if fx == fy {
return false
}
if uf.rank[fx] < uf.rank[fy] {
fx, fy = fy, fx
}
uf.rank[fx] += uf.rank[fy]
uf.parent[fy] = fx
return true
}
func dist(p, q []int) int {
return abs(p[0]-q[0]) + abs(p[1]-q[1])
}
func minCostConnectPoints(points [][]int) (ans int) {
n := len(points)
type edge struct{ v, w, dis int }
edges := []edge{}
for i, p := range points {
for j := i + 1; j < n; j++ {
edges = append(edges, edge{i, j, dist(p, points[j])})
}
}
sort.Slice(edges, func(i, j int) bool { return edges[i].dis < edges[j].dis })
uf := newUnionFind(n)
left := n - 1
for _, e := range edges {
if uf.union(e.v, e.w) {
ans += e.dis
left--
if left == 0 {
break
}
}
}
return
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
python3 解法, 执行用时: 1296 ms, 内存消耗: 81.1 MB, 提交时间: 2022-11-27 11:35:39
class DisjointSetUnion:
def __init__(self, n):
self.n = n
self.rank = [1] * n
self.f = list(range(n))
def find(self, x: int) -> int:
if self.f[x] == x:
return x
self.f[x] = self.find(self.f[x])
return self.f[x]
def unionSet(self, x: int, y: int) -> bool:
fx, fy = self.find(x), self.find(y)
if fx == fy:
return False
if self.rank[fx] < self.rank[fy]:
fx, fy = fy, fx
self.rank[fx] += self.rank[fy]
self.f[fy] = fx
return True
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
dist = lambda x, y: abs(points[x][0] - points[y][0]) + abs(points[x][1] - points[y][1])
n = len(points)
dsu = DisjointSetUnion(n)
edges = list()
for i in range(n):
for j in range(i + 1, n):
edges.append((dist(i, j), i, j))
edges.sort()
ret, num = 0, 1
for length, x, y in edges:
if dsu.unionSet(x, y):
ret += length
num += 1
if num == n:
break
return ret
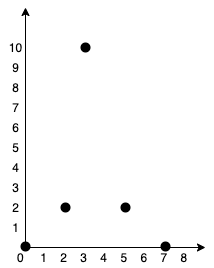
我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。 注意到任意两个点之间只有唯一一条路径互相到达。