C++
Java
Python
Python3
C
C#
JavaScript
Ruby
Swift
Go
Scala
Kotlin
Rust
PHP
TypeScript
Racket
monokai
ambiance
chaos
chrome
cloud9_day
cloud9_night
cloud9_night_low_color
clouds
clouds_midnight
cobalt
crimson_editor
dawn
dracula
dreamweaver
eclipse
github
github_dark
gob
gruvbox
gruvbox_dark_hard
gruvbox_light_hard
idle_fingers
iplastic
katzenmilch
kr_theme
kuroir
merbivore
merbivore_soft
mono_industrial
nord_dark
one_dark
pastel_on_dark
solarized_dark
solarized_light
sqlserver
terminal
textmate
tomorrow
tomorrow_night
tomorrow_night_blue
tomorrow_night_bright
tomorrow_night_eighties
twilight
vibrant_ink
xcode
上次编辑到这里,代码来自缓存 点击恢复默认模板
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* canMerge(vector<TreeNode*>& trees) {
}
};
运行代码
提交
golang 解法, 执行用时: 332 ms, 内存消耗: 20.5 MB, 提交时间: 2023-09-23 11:06:19
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
const mx int = 5e4 + 1
func canMerge(trees []*TreeNode) *TreeNode {
isSub := [mx]bool{} // 对于根节点,需要知道其是否为另一颗二叉搜索树的子节点
roots := [mx]*TreeNode{} // 对于子节点,我们需要知道其数值所对应的二叉搜索树的根节点是哪个
for _, rt := range trees {
if rt.Left != nil {
if isSub[rt.Left.Val] { // 由于二叉搜索树上不能有两个值相同的节点,所以 trees 中也不能有两个值相同的子节点
return nil
}
isSub[rt.Left.Val] = true
}
if rt.Right != nil {
if isSub[rt.Right.Val] {
return nil
}
isSub[rt.Right.Val] = true
}
roots[rt.Val] = rt
}
var root *TreeNode
for _, rt := range trees {
if !isSub[rt.Val] { // 根节点不应是另一颗二叉搜索树的子节点,否则二叉搜索树上会出现两个值相同的节点
if root != nil { // 根节点应只有一个,否则会构成森林
return nil
}
root = rt
}
}
if root == nil { // 未找到根节点
return nil
}
cnt := 0
// 在构建二叉搜索树的同时判断是否合法
var build func(*TreeNode, int, int) *TreeNode
build = func(node *TreeNode, l, r int) *TreeNode {
cnt++
if node.Left != nil {
if node.Left.Val <= l {
return nil
}
if lo := roots[node.Left.Val]; lo != nil {
node.Left = build(lo, l, node.Val)
if node.Left == nil {
return nil
}
}
}
if node.Right != nil {
if node.Right.Val >= r {
return nil
}
if ro := roots[node.Right.Val]; ro != nil {
node.Right = build(ro, node.Val, r)
if node.Right == nil {
return nil
}
}
}
return node
}
root = build(root, 0, mx)
if cnt == len(trees) { // 所有 trees[i] 均参与构建二叉搜索树
return root
}
return nil
}
java 解法, 执行用时: 37 ms, 内存消耗: 68.2 MB, 提交时间: 2023-09-23 11:05:58
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
// 存储所有叶节点值的哈希集合
HashSet<Integer> leaves = new HashSet<>();
// 存储 (根节点值, 树) 键值对的哈希映射
HashMap<Integer, TreeNode> candidates = new HashMap<>();
// 在中序遍历中存储中序遍历上一个遍历到的值,便于检查严格单调性
int prev = 0;
public TreeNode canMerge(List<TreeNode> trees) {
for (TreeNode tree : trees) {
if (tree.left != null) {
leaves.add(tree.left.val);
}
if (tree.right != null) {
leaves.add(tree.right.val);
}
candidates.put(tree.val, tree);
}
for (TreeNode tree : trees) {
// 寻找合并完成后的树的根节点
if (!leaves.contains(tree.val)) {
// 将其从哈希映射中移除
candidates.remove(tree.val);
// 从根节点开始进行遍历
// 如果中序遍历有严格单调性,并且所有树的根节点都被遍历到,说明可以构造二叉搜索树
prev = 0;
return (dfs(tree) && candidates.isEmpty()) ? tree : null;
}
}
return null;
}
// 中序遍历,返回值表示是否有严格单调性
private boolean dfs(TreeNode tree) {
if (tree == null) {
return true;
}
// 如果遍历到叶节点,并且存在可以合并的树,那么就进行合并
if (tree.left == null && tree.right == null && candidates.containsKey(tree.val)) {
tree.left = candidates.get(tree.val).left;
tree.right = candidates.get(tree.val).right;
// 合并完成后,将树从哈希映射中移除,以便于在遍历结束后判断是否所有树都被遍历过
candidates.remove(tree.val);
}
// 先遍历左子树
if (!dfs(tree.left)) {
return false;
}
// 再遍历当前节点
if (tree.val <= prev) {
return false;
}
prev = tree.val;
// 最后遍历右子树
return dfs(tree.right);
}
}
python3 解法, 执行用时: 1780 ms, 内存消耗: 67.3 MB, 提交时间: 2023-09-23 11:05:40
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def canMerge(self, trees: List[TreeNode]) -> Optional[TreeNode]:
# 存储所有叶节点值的哈希集合
leaves = set()
# 存储 (根节点值, 树) 键值对的哈希映射
candidates = dict()
for tree in trees:
if tree.left:
leaves.add(tree.left.val)
if tree.right:
leaves.add(tree.right.val)
candidates[tree.val] = tree
# 存储中序遍历上一个遍历到的值,便于检查严格单调性
prev = float("-inf")
# 中序遍历,返回值表示是否有严格单调性
def dfs(tree: Optional[TreeNode]) -> bool:
if not tree:
return True
# 如果遍历到叶节点,并且存在可以合并的树,那么就进行合并
if not tree.left and not tree.right and tree.val in candidates:
tree.left = candidates[tree.val].left
tree.right = candidates[tree.val].right
# 合并完成后,将树丛哈希映射中移除,以便于在遍历结束后判断是否所有树都被遍历过
candidates.pop(tree.val)
# 先遍历左子树
if not dfs(tree.left):
return False
# 再遍历当前节点
nonlocal prev
if tree.val <= prev:
return False
prev = tree.val
# 最后遍历右子树
return dfs(tree.right)
for tree in trees:
# 寻找合并完成后的树的根节点
if tree.val not in leaves:
# 将其从哈希映射中移除
candidates.pop(tree.val)
# 从根节点开始进行遍历
# 如果中序遍历有严格单调性,并且所有树的根节点都被遍历到,说明可以构造二叉搜索树
return tree if dfs(tree) and not candidates else None
return None
cpp 解法, 执行用时: 928 ms, 内存消耗: 422.9 MB, 提交时间: 2023-09-23 11:05:27
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* canMerge(vector<TreeNode*>& trees) {
// 存储所有叶节点值的哈希集合
unordered_set<int> leaves;
// 存储 (根节点值, 树) 键值对的哈希映射
unordered_map<int, TreeNode*> candidates;
for (TreeNode* tree: trees) {
if (tree->left) {
leaves.insert(tree->left->val);
}
if (tree->right) {
leaves.insert(tree->right->val);
}
candidates[tree->val] = tree;
}
// 存储中序遍历上一个遍历到的值,便于检查严格单调性
int prev = 0;
// 中序遍历,返回值表示是否有严格单调性
function<bool(TreeNode*)> dfs = [&](TreeNode* tree) {
if (!tree) {
return true;
}
// 如果遍历到叶节点,并且存在可以合并的树,那么就进行合并
if (!tree->left && !tree->right && candidates.count(tree->val)) {
tree->left = candidates[tree->val]->left;
tree->right = candidates[tree->val]->right;
// 合并完成后,将树从哈希映射中移除,以便于在遍历结束后判断是否所有树都被遍历过
candidates.erase(tree->val);
}
// 先遍历左子树
if (!dfs(tree->left)) {
return false;
}
// 再遍历当前节点
if (tree->val <= prev) {
return false;
};
prev = tree->val;
// 最后遍历右子树
return dfs(tree->right);
};
for (TreeNode* tree: trees) {
// 寻找合并完成后的树的根节点
if (!leaves.count(tree->val)) {
// 将其从哈希映射中移除
candidates.erase(tree->val);
// 从根节点开始进行遍历
// 如果中序遍历有严格单调性,并且所有树的根节点都被遍历到,说明可以构造二叉搜索树
return (dfs(tree) && candidates.empty()) ? tree : nullptr;
}
}
return nullptr;
}
};
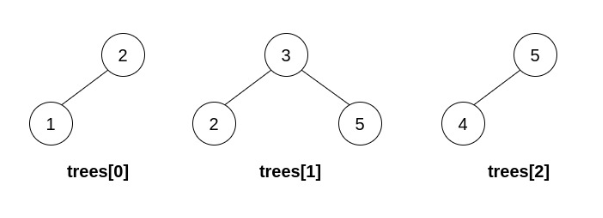
在第二步操作中,选出 i=0 和 j=1 ,将 trees[1] 合并到 trees[0] 中。 删除 trees[1] ,trees = [[3,2,5,1,null,4]] 。
结果树如上图所示,为一棵有效的二叉搜索树,所以返回该树的根节点。
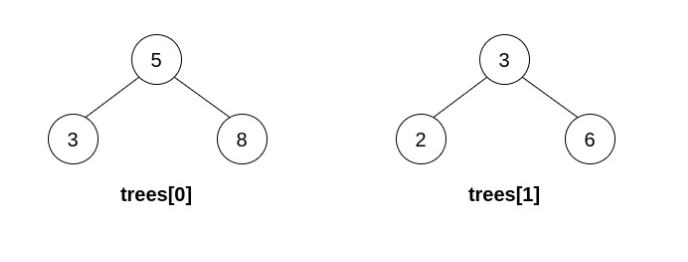
结果树如上图所示。仅能执行一次有效的操作,但结果树不是一棵有效的二叉搜索树,所以返回 null 。