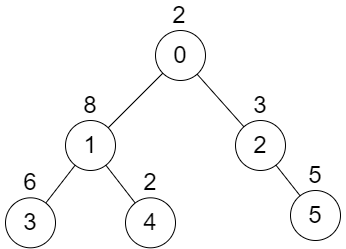
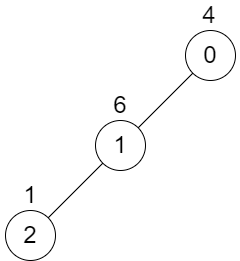
C++
Java
Python
Python3
C
C#
JavaScript
TypeScript
PHP
Swift
Kotlin
Dart
Go
Ruby
Scala
Rust
Racket
Erlang
Elixir
monokai
ambiance
chaos
chrome
cloud9_day
cloud9_night
cloud9_night_low_color
clouds
clouds_midnight
cobalt
crimson_editor
dawn
dracula
dreamweaver
eclipse
github
github_dark
gob
gruvbox
gruvbox_dark_hard
gruvbox_light_hard
idle_fingers
iplastic
katzenmilch
kr_theme
kuroir
merbivore
merbivore_soft
mono_industrial
nord_dark
one_dark
pastel_on_dark
solarized_dark
solarized_light
sqlserver
terminal
textmate
tomorrow
tomorrow_night
tomorrow_night_blue
tomorrow_night_bright
tomorrow_night_eighties
twilight
vibrant_ink
xcode
上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
long long maxXor(int n, vector<vector<int>>& edges, vector<int>& values) {
}
};
运行代码
提交
java 解法, 执行用时: 80 ms, 内存消耗: 87.6 MB, 提交时间: 2023-10-21 20:16:46
class Solution {
class TrieNode{
TrieNode[] child = new TrieNode[2];
}
TrieNode root = new TrieNode();
int bits = 46;
long[] s;
long res = 0;
List<List<Integer>> adj = new ArrayList<>();
void add(long val){
TrieNode node = root;
for(int i = bits; i >= 0; i -- ){
int cur = (int)((val >> i) & 1);
if(node.child[cur] == null) node.child[cur] = new TrieNode();
node = node.child[cur];
}
}
long query(long val){
TrieNode node = root;
long res = 0;
for(int i = bits; i >= 0; i -- ){
int cur = (int)((val >> i) & 1);
if(node.child[1-cur] != null){
res = res + (1l << i);
node = node.child[1-cur];
}else if(node.child[cur] != null){
node = node.child[cur];
}else{
return res;
}
}
return res;
}
long dfs(int node, int prev, int[] values){
long res = values[node];
for(var e: adj.get(node)){
if(e.equals(prev)) continue;
res += dfs((int) e, node, values);
}
s[node] = res;
return res;
}
void process(int node, int prev){
long ans = query(s[node]);
if(ans > res) res = ans;
for(var next: adj.get(node)){
if(next.equals(prev)) continue;
process(next, node);
}
add(s[node]);
}
public long maxXor(int n, int[][] edges, int[] values) {
s = new long[n];
for(int i = 0; i < n; i ++ ){
adj.add(new ArrayList<>());
}
for(int i = 0; i < edges.length; i ++ ){
adj.get(edges[i][0]).add(edges[i][1]);
adj.get(edges[i][1]).add(edges[i][0]);
}
dfs(0, -1, values);
process(0, -1);
return res;
}
}
cpp 解法, 执行用时: 296 ms, 内存消耗: 88.5 MB, 提交时间: 2023-10-21 20:16:06
class Trie {
private:
int L;
Trie* left;
Trie* right;
public:
Trie() : L(47), left(nullptr), right(nullptr) {}
void insert(long long val) {
Trie* node = this;
for (int i = L; i >= 0; i--) {
if (!(val >> i & 1)) {
if (node->left == nullptr) {
node->left = new Trie();
}
node = node->left;
} else {
if (node->right == nullptr) {
node->right = new Trie();
}
node = node->right;
}
}
}
long long query_maxor(long long val) {
Trie* node = this;
long long ans = 0;
for (int i = L; i >= 0; i--) {
if (node == nullptr) {
return ans;
}
if (val >> i & 1) {
if (node->left != nullptr) {
ans |= 1ll << i;
node = node->left;
} else {
node = node->right;
}
} else {
if (node->right != nullptr) {
ans |= 1ll << i;
node = node->right;
} else {
node = node->left;
}
}
}
return ans;
}
};
class Solution {
public:
long long maxXor(int n, vector<vector<int>>& edges, vector<int>& values) {
// 建图
vector<vector<int>> graph(n);
for (auto& e: edges) {
graph[e[0]].push_back(e[1]);
graph[e[1]].push_back(e[0]);
}
// 预处理子树和
vector<long long> s(n);
function<long long(int, int)> dfs1 = [&] (int node, int fa) -> long long {
long long tot = values[node];
for (auto& nxt: graph[node]) {
if (nxt == fa) continue;
tot += dfs1(nxt, node);
}
s[node] = tot;
return tot;
};
dfs1(0, -1);
// 遍历子树和,求最大异或值
long long ans = 0;
Trie tree;
function<void(int, int)> dfs2 = [&] (int node, int fa) {
ans = max(ans, tree.query_maxor(s[node]));
for (auto& nxt: graph[node]) {
if (nxt == fa) continue;
dfs2(nxt, node);
}
tree.insert(s[node]);
};
dfs2(0, -1);
return ans;
}
};
python3 解法, 执行用时: 2344 ms, 内存消耗: 173.8 MB, 提交时间: 2023-10-21 20:15:48
class Trie:
def __init__(self):
self.L = 47
self.left = None
self.right = None
def insert(self, val: int) -> None:
node = self
for i in range(self.L, -1, -1):
if not val & (1 << i):
if not node.left:
node.left = Trie()
node = node.left
else:
if not node.right:
node.right = Trie()
node = node.right
def query_maxor(self, val: int) -> int:
node = self
ans = 0
for i in range(self.L, -1, -1):
if not node:
return ans
if val & (1 << i):
if node.left:
ans |= (1 << i)
node = node.left
else:
node = node.right
else:
if node.right:
ans |= (1 << i)
node = node.right
else:
node = node.left
return ans
class Solution:
def maxXor(self, n: int, edges: List[List[int]], values: List[int]) -> int:
# 建图
graph = defaultdict(list)
for u, v in edges:
graph[u].append(v)
graph[v].append(u)
# 预处理子树和
s = [0] * n
def dfs1(node: int, fa: int) -> int:
ans = values[node]
for nxt in graph[node]:
if nxt == fa: continue
ans += dfs1(nxt, node)
s[node] = ans
return ans
dfs1(0, -1)
# 遍历子树和,求最大异或值
ans = 0
tree = Trie()
def dfs2(node: int, fa: int):
nonlocal ans
ans = max(ans, tree.query_maxor(s[node]))
for nxt in graph[node]:
if nxt == fa: continue
dfs2(nxt, node)
tree.insert(s[node])
dfs2(0, -1)
return ans