列表

详情

2271. 毯子覆盖的最多白色砖块数

给你一个二维整数数组 tiles ，其中 tiles[i] = [li, ri] ，表示所有在 li <= j <= ri 之间的每个瓷砖位置 j 都被涂成了白色。

同时给你一个整数 carpetLen ，表示可以放在 任何位置 的一块毯子。

请你返回使用这块毯子，最多 可以盖住多少块瓷砖。

 

示例 1：

输入：tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10
输出：9
解释：将毯子从瓷砖 10 开始放置。
总共覆盖 9 块瓷砖，所以返回 9 。
注意可能有其他方案也可以覆盖 9 块瓷砖。
可以看出，瓷砖无法覆盖超过 9 块瓷砖。

示例 2：

输入：tiles = [[10,11],[1,1]], carpetLen = 2
输出：2
解释：将毯子从瓷砖 10 开始放置。
总共覆盖 2 块瓷砖，所以我们返回 2 。

 

提示：

原站题解

去查看

上次编辑到这里，代码来自缓存 点击恢复默认模板
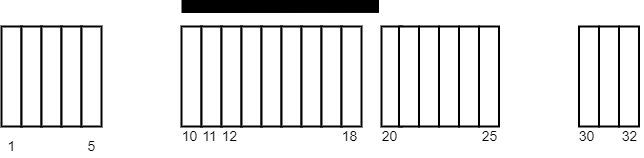
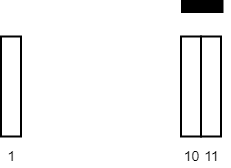
class Solution { public: int maximumWhiteTiles(vector<vector<int>>& tiles, int carpetLen) { } };

cpp 解法, 执行用时: 336 ms, 内存消耗: 68.8 MB, 提交时间: 2023-09-27 09:36:05 

class Solution {
public:
    int maximumWhiteTiles(vector<vector<int>>& tiles, int carpetLen) {
        sort(tiles.begin(), tiles.end());   // 按照起始位置排序
        int n = tiles.size();
        int res = 0;   // 最多可以覆盖的瓷砖数量
        int cnt = 0;   // 当前可以完全覆盖的连续瓷砖段的瓷砖数总和
        int r = 0;   // 从左至右第一段无法完全覆盖的连续瓷砖的下标
        // 枚举起始点对应连续瓷砖段的下标
        for (int l = 0; l < n; ++l) {
            if (l) {
                cnt -= tiles[l-1][1] - tiles[l-1][0] + 1;
            }
            while (r < n && tiles[l][0] + carpetLen > tiles[r][1]) {
                cnt += tiles[r][1] - tiles[r][0] + 1;
                ++r;
            }
            if (r == n) {
                // 此时无法通过右移增加覆盖瓷砖数，更新最大值并返回即可
                res = max(res, cnt);
                return res;
            }
            int extra = max(0, tiles[l][0] + carpetLen - tiles[r][0]);   // 当前无法完全覆盖的连续瓷砖段的覆盖瓷砖数
            res = max(res, cnt + extra);
        }
        return res;
    }
};

python3 解法, 执行用时: 216 ms, 内存消耗: 36.6 MB, 提交时间: 2023-09-27 09:35:47 

class Solution:
    def maximumWhiteTiles(self, tiles: List[List[int]], carpetLen: int) -> int:
        tiles.sort()   # 按照左端点排序
        n = len(tiles)
        res = 0   # 最多可以覆盖的瓷砖数量
        cnt = 0   # 当前可以完全覆盖的连续瓷砖段的瓷砖数总和
        r = 0   # 从左至右第一段无法完全覆盖的连续瓷砖的下标
        # 枚举起始点对应连续瓷砖段的下标
        for l in range(n):
            if l > 0:
                cnt -= tiles[l-1][1] - tiles[l-1][0] + 1
            while r < n and tiles[l][0] + carpetLen > tiles[r][1]:  # 能覆盖当前这段瓷砖区间
                cnt += tiles[r][1] - tiles[r][0] + 1
                r += 1
            if r == n:
                # 此时无法通过右移增加覆盖瓷砖数，更新最大值并返回即可
                res = max(res, cnt)
                return res
            extra = max(0, tiles[l][0] + carpetLen - tiles[r][0])   # 当前无法完全覆盖的连续瓷砖段的覆盖瓷砖数
            res = max(res, cnt + extra)
        return res

golang 解法, 执行用时: 180 ms, 内存消耗: 12.3 MB, 提交时间: 2023-09-27 09:32:24 

func maximumWhiteTiles(tiles [][]int, carpetLen int) (ans int) {
	sort.Slice(tiles, func(i, j int) bool { return tiles[i][0] < tiles[j][0] })
	cover, left := 0, 0
	for _, t := range tiles {
		tl, tr := t[0], t[1]
		cover += tr - tl + 1
		for tiles[left][1]+carpetLen-1 < tr {
			cover -= tiles[left][1] - tiles[left][0] + 1
			left++
		}
		ans = max(ans, cover-max(tr-carpetLen+1-tiles[left][0], 0)) // 0 表示毯子左端点不在瓷砖内的情况
	}
	return
}

func max(a, b int) int { if b > a { return b }; return a }

cpp 解法, 执行用时: 280 ms, 内存消耗: 68.6 MB, 提交时间: 2023-09-27 09:31:59 

class Solution {
public:
    int maximumWhiteTiles(vector<vector<int>> &tiles, int carpetLen) {
        sort(tiles.begin(), tiles.end(), [](auto &a, auto &b) { return a[0] < b[0]; });
        int ans = 0, cover = 0, left = 0;
        for (auto &t : tiles) {
            int tl = t[0], tr = t[1];
            cover += tr - tl + 1;
            for (; tiles[left][1] + carpetLen - 1 < tr; ++left)
                cover -= tiles[left][1] - tiles[left][0] + 1;
            ans = max(ans, cover - max(tr - carpetLen + 1 - tiles[left][0], 0)); // 0 表示毯子左端点不在瓷砖内的情况
        }
        return ans;
    }
};

java 解法, 执行用时: 44 ms, 内存消耗: 69.2 MB, 提交时间: 2023-09-27 09:31:38 

class Solution {
    public int maximumWhiteTiles(int[][] tiles, int carpetLen) {
        Arrays.sort(tiles, (a, b) -> a[0] - b[0]);
        int ans = 0, cover = 0, left = 0;
        for (var t : tiles) {
            int tl = t[0], tr = t[1];
            cover += tr - tl + 1;
            for (; tiles[left][1] + carpetLen - 1 < tr; ++left)
                cover -= tiles[left][1] - tiles[left][0] + 1;
            ans = Math.max(ans, cover - Math.max(tr - carpetLen + 1 - tiles[left][0], 0)); // 0 表示毯子左端点不在瓷砖内的情况
        }
        return ans;
    }
}

python3 解法, 执行用时: 296 ms, 内存消耗: 36.9 MB, 提交时间: 2023-09-27 09:31:12 

'''
瓷砖按左端点排序，然后枚举毯子位置
'''
class Solution:
    def maximumWhiteTiles(self, tiles: List[List[int]], carpetLen: int) -> int:
        tiles.sort(key=lambda x: x[0])
        ans = cover = left = 0
        for tl, tr in tiles:
            cover += tr - tl + 1
            while tiles[left][1] < tr - carpetLen + 1:
                cover -= tiles[left][1] - tiles[left][0] + 1
                left += 1
            ans = max(ans, cover - max(tr - carpetLen + 1 - tiles[left][0], 0))  # 0 表示毯子左端点不在瓷砖内的情况
        return ans

上一题

© 2024 leetcode.cn