java 解法, 执行用时: 0 ms, 内存消耗: 39 MB, 提交时间: 2023-09-07 00:06:18
class Solution {
public int numMagicSquaresInside(int[][] grid) {
int R = grid.length, C = grid[0].length;
int ans = 0;
for (int r = 0; r < R-2; ++r)
for (int c = 0; c < C-2; ++c) {
if (grid[r+1][c+1] != 5) continue; // optional skip
if (magic(grid[r][c], grid[r][c+1], grid[r][c+2],
grid[r+1][c], grid[r+1][c+1], grid[r+1][c+2],
grid[r+2][c], grid[r+2][c+1], grid[r+2][c+2]))
ans++;
}
return ans;
}
public boolean magic(int... vals) {
int[] count = new int[16];
for (int v: vals) count[v]++;
for (int v = 1; v <= 9; ++v)
if (count[v] != 1)
return false;
return (vals[0] + vals[1] + vals[2] == 15 &&
vals[3] + vals[4] + vals[5] == 15 &&
vals[6] + vals[7] + vals[8] == 15 &&
vals[0] + vals[3] + vals[6] == 15 &&
vals[1] + vals[4] + vals[7] == 15 &&
vals[2] + vals[5] + vals[8] == 15 &&
vals[0] + vals[4] + vals[8] == 15 &&
vals[2] + vals[4] + vals[6] == 15);
}
}
python3 解法, 执行用时: 32 ms, 内存消耗: 16.1 MB, 提交时间: 2023-09-07 00:05:32
class Solution:
def numMagicSquaresInside(self, grid: List[List[int]]) -> int:
R, C = len(grid), len(grid[0])
def magic(a: int, b: int, c: int, d: int, e: int, f: int, g: int, h: int, i: int) -> bool:
return (sorted([a,b,c,d,e,f,g,h,i]) == list(range(1, 10)) and
(a+b+c == d+e+f == g+h+i == a+d+g == b+e+h == c+f+i == a+e+i == c+e+g == 15))
ans = 0
for r in range(R-2):
for c in range(C-2):
if grid[r+1][c+1] != 5: continue # optional skip
if magic(grid[r][c], grid[r][c+1], grid[r][c+2],
grid[r+1][c], grid[r+1][c+1], grid[r+1][c+2],
grid[r+2][c], grid[r+2][c+1], grid[r+2][c+2]):
ans += 1
return ans
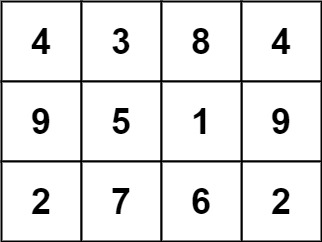
而这一个不是:
总的来说,在本示例所给定的矩阵中只有一个 3 x 3 的幻方子矩阵。