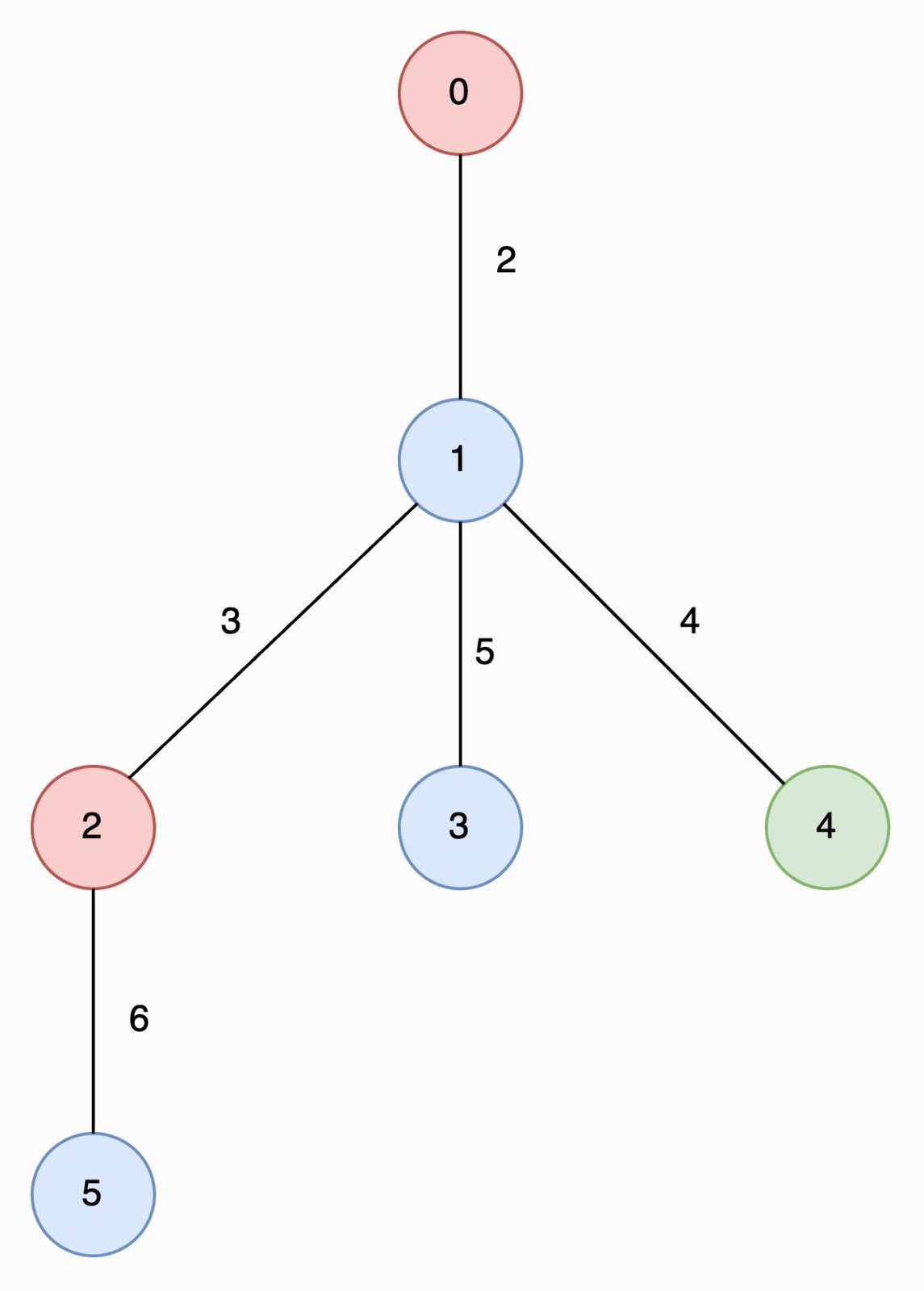
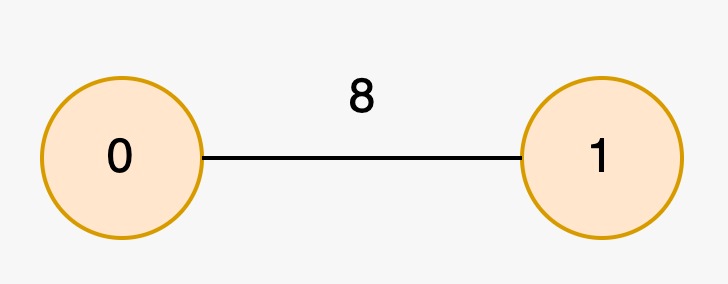
上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
vector<int> longestSpecialPath(vector<vector<int>>& edges, vector<int>& nums) {
}
};
golang 解法, 执行用时: 112 ms, 内存消耗: 42.8 MB, 提交时间: 2025-01-25 12:56:03
func longestSpecialPath(edges [][]int, nums []int) []int {
type edge struct{ to, weight int }
g := make([][]edge, len(nums))
for _, e := range edges {
x, y, w := e[0], e[1], e[2]
g[x] = append(g[x], edge{y, w})
g[y] = append(g[y], edge{x, w})
}
maxLen := -1
minNodes := 0
dis := []int{0}
// 颜色 -> 该颜色最近一次出现的深度 +1,注意这里已经 +1 了
lastDepth := map[int]int{}
var dfs func(int, int, int)
dfs = func(x, fa, topDepth int) {
color := nums[x]
oldDepth := lastDepth[color]
topDepth = max(topDepth, oldDepth)
length := dis[len(dis)-1] - dis[topDepth]
nodes := len(dis) - topDepth
if length > maxLen || length == maxLen && nodes < minNodes {
maxLen = length
minNodes = nodes
}
lastDepth[color] = len(dis)
for _, e := range g[x] {
y := e.to
if y != fa { // 避免访问父节点
dis = append(dis, dis[len(dis)-1]+e.weight)
dfs(y, x, topDepth)
dis = dis[:len(dis)-1] // 恢复现场
}
}
lastDepth[color] = oldDepth // 恢复现场
}
dfs(0, -1, 0)
return []int{maxLen, minNodes}
}
java 解法, 执行用时: 57 ms, 内存消耗: 90.6 MB, 提交时间: 2025-01-25 12:55:49
class Solution {
private int maxLen = -1;
private int minNodes = 0;
public int[] longestSpecialPath(int[][] edges, int[] nums) {
List<int[]>[] g = new ArrayList[nums.length];
Arrays.setAll(g, i -> new ArrayList<>());
for (int[] e : edges) {
int x = e[0];
int y = e[1];
int w = e[2];
g[x].add(new int[]{y, w});
g[y].add(new int[]{x, w});
}
List<Integer> dis = new ArrayList<>();
dis.add(0);
// 颜色 -> 该颜色最近一次出现的深度 +1,注意这里已经 +1 了
Map<Integer, Integer> lastDepth = new HashMap<>();
dfs(0, -1, 0, g, nums, dis, lastDepth);
return new int[]{maxLen, minNodes};
}
private void dfs(int x, int fa, int topDepth, List<int[]>[] g, int[] nums, List<Integer> dis, Map<Integer, Integer> lastDepth) {
int color = nums[x];
int oldDepth = lastDepth.getOrDefault(color, 0);
topDepth = Math.max(topDepth, oldDepth);
int disX = dis.get(dis.size() - 1);
int len = disX - dis.get(topDepth);
int nodes = dis.size() - topDepth;
if (len > maxLen || len == maxLen && nodes < minNodes) {
maxLen = len;
minNodes = nodes;
}
lastDepth.put(color, dis.size());
for (int[] e : g[x]) {
int y = e[0];
if (y != fa) { // 避免访问父节点
dis.add(disX + e[1]);
dfs(y, x, topDepth, g, nums, dis, lastDepth);
dis.remove(dis.size() - 1); // 恢复现场
}
}
lastDepth.put(color, oldDepth); // 恢复现场
}
}
cpp 解法, 执行用时: 1429 ms, 内存消耗: 235.5 MB, 提交时间: 2025-01-25 12:55:36
class Solution {
public:
vector<int> longestSpecialPath(vector<vector<int>>& edges, vector<int>& nums) {
vector<vector<pair<int, int>>> g(nums.size());
for (auto& e : edges) {
int x = e[0], y = e[1], w = e[2];
g[x].emplace_back(y, w);
g[y].emplace_back(x, w);
}
pair<int, int> ans = {-1, 0};
vector<int> dis = {0};
unordered_map<int, int> last_depth; // 颜色 -> 该颜色最近一次出现的深度 +1,注意这里已经 +1 了
auto dfs = [&](this auto&& dfs, int x, int fa, int top_depth) -> void {
int color = nums[x];
int old_depth = last_depth[color];
top_depth = max(top_depth, old_depth);
// 把 dis.size() - top_depth 取反,这样 max 算的是最小值
ans = max(ans, pair(dis.back() - dis[top_depth], top_depth - (int) dis.size()));
last_depth[color] = dis.size();
for (auto& [y, w] : g[x]) {
if (y != fa) { // 避免访问父节点
dis.push_back(dis.back() + w);
dfs(y, x, top_depth);
dis.pop_back(); // 恢复现场
}
}
last_depth[color] = old_depth; // 恢复现场
};
dfs(0, -1, 0);
return {ans.first, -ans.second};
}
};
cpp 解法, 执行用时: 186 ms, 内存消耗: 228.1 MB, 提交时间: 2025-01-25 12:55:23
class Solution {
vector<int> nums;
vector<vector<pair<int, int>>> g;
pair<int, int> ans = {-1, 0};
vector<int> dis = {0};
unordered_map<int, int> last_depth; // 颜色 -> 该颜色最近一次出现的深度 +1,注意这里已经 +1 了
void dfs(int x, int fa, int top_depth) {
int color = nums[x];
int old_depth = last_depth[color];
top_depth = max(top_depth, old_depth);
// 把 dis.size() - top_depth 取反,这样 max 算的是最小值
ans = max(ans, pair(dis.back() - dis[top_depth], top_depth - (int) dis.size()));
last_depth[color] = dis.size();
for (auto& [y, w] : g[x]) {
if (y != fa) { // 避免访问父节点
dis.push_back(dis.back() + w);
dfs(y, x, top_depth);
dis.pop_back(); // 恢复现场
}
}
last_depth[color] = old_depth; // 恢复现场
}
public:
vector<int> longestSpecialPath(vector<vector<int>>& edges, vector<int>& nums) {
g.resize(nums.size());
for (auto& e : edges) {
int x = e[0], y = e[1], w = e[2];
g[x].emplace_back(y, w);
g[y].emplace_back(x, w);
}
this->nums = nums;
dfs(0, -1, 0);
return {ans.first, -ans.second};
}
};
python3 解法, 执行用时: 365 ms, 内存消耗: 64.1 MB, 提交时间: 2025-01-25 12:55:11
class Solution:
def longestSpecialPath(self, edges: List[List[int]], nums: List[int]) -> List[int]:
g = [[] for _ in nums]
for x, y, w in edges:
g[x].append((y, w))
g[y].append((x, w))
ans = (-1, 0)
dis = [0]
last_depth = {} # 颜色 -> 该颜色最近一次出现的深度 +1,注意这里已经 +1 了
def dfs(x: int, fa: int, top_depth: int) -> None:
color = nums[x]
old_depth = last_depth.get(color, 0)
top_depth = max(top_depth, old_depth)
nonlocal ans
# 把 len(dis) - top_depth 取反,这样 max 算的是最小值
ans = max(ans, (dis[-1] - dis[top_depth], top_depth - len(dis)))
last_depth[color] = len(dis)
for y, w in g[x]:
if y != fa: # 避免访问父节点
dis.append(dis[-1] + w)
dfs(y, x, top_depth)
dis.pop() # 恢复现场
last_depth[color] = old_depth # 恢复现场
dfs(0, -1, 0)
return [ans[0], -ans[1]]