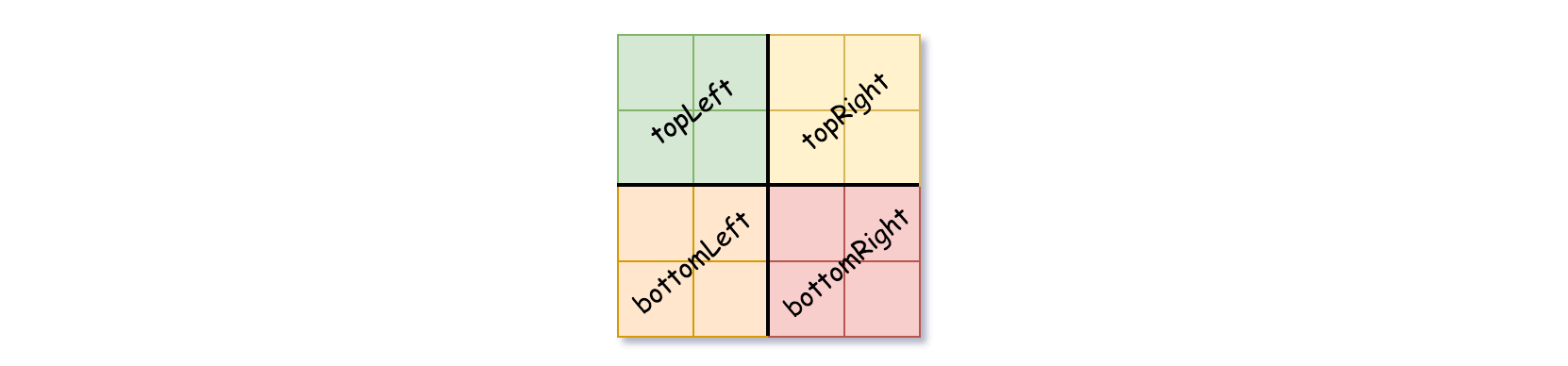
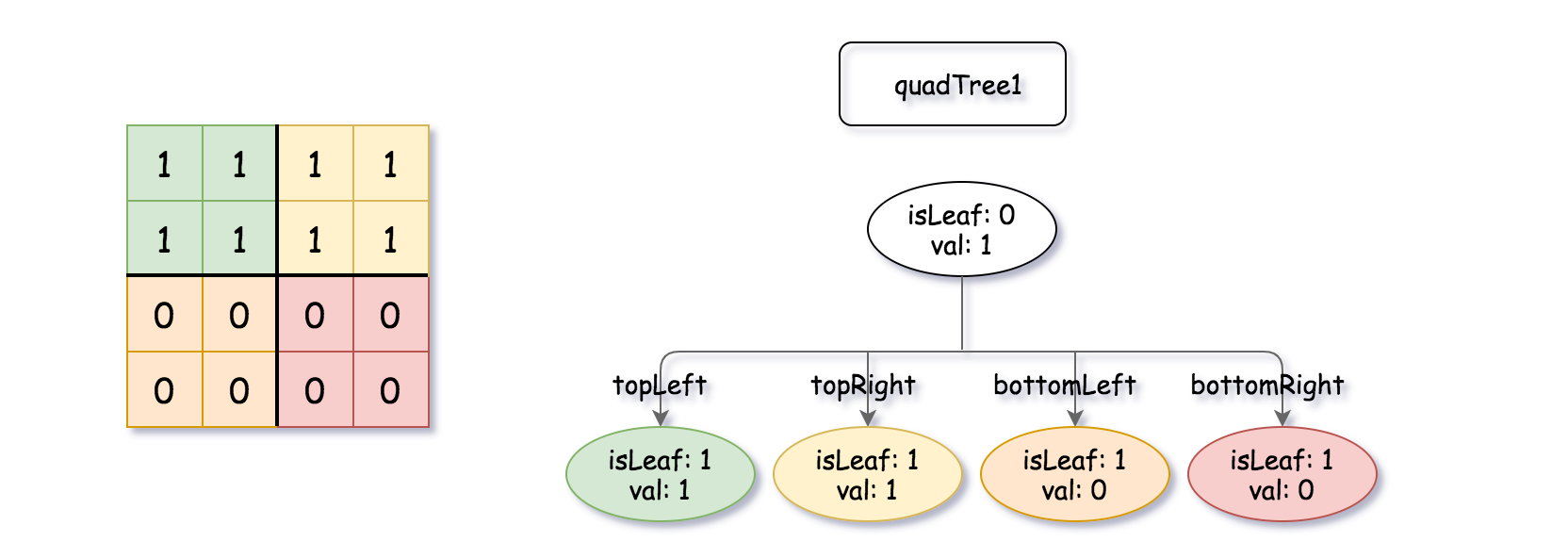
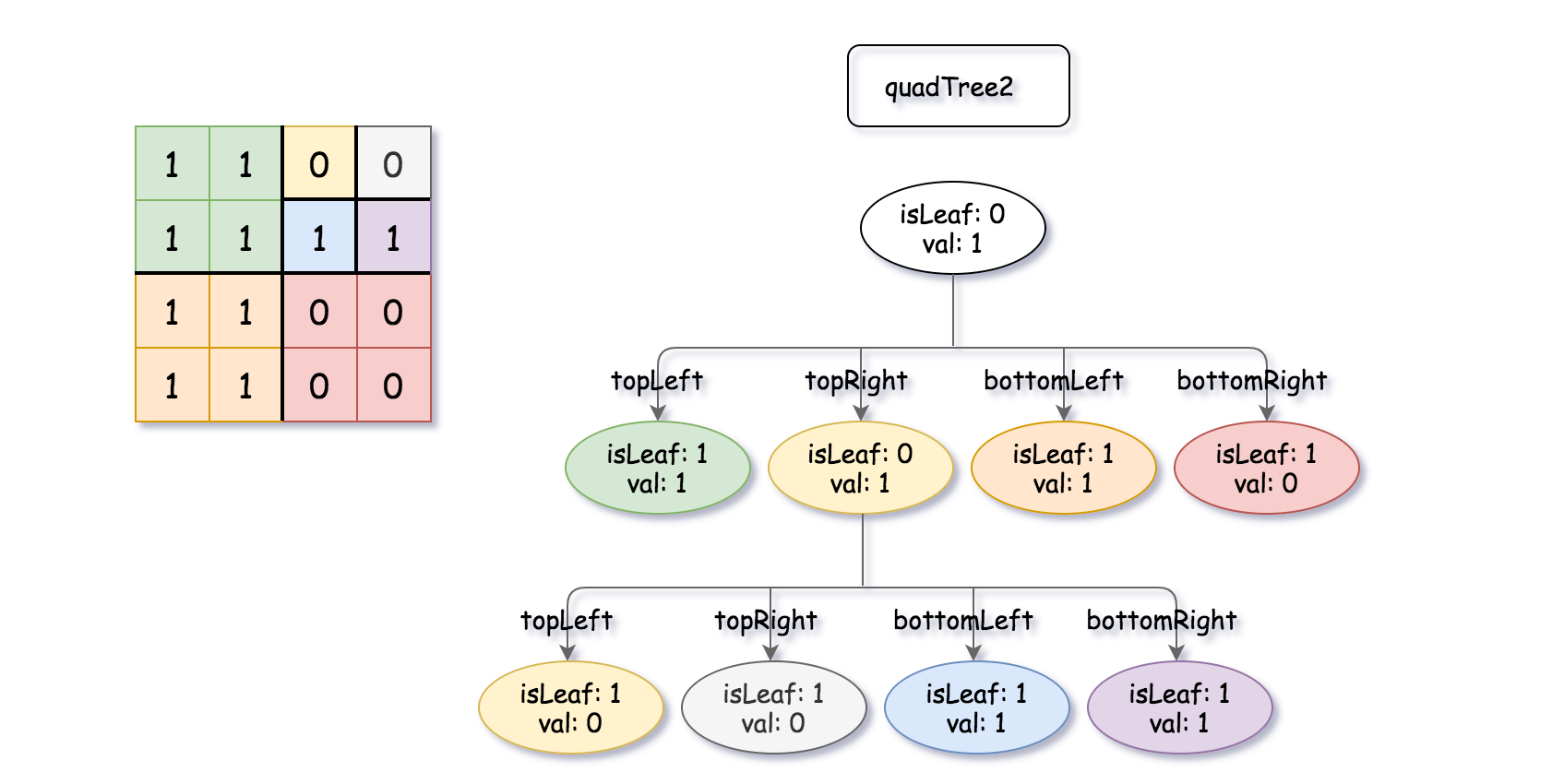
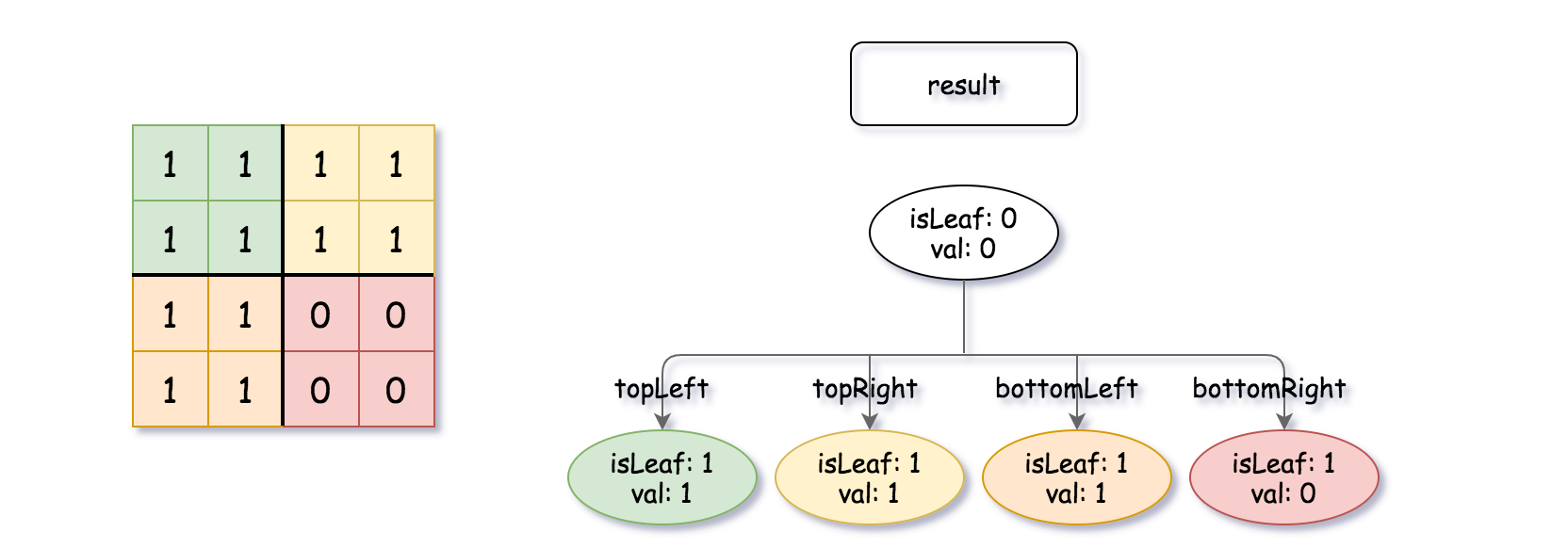
上次编辑到这里,代码来自缓存 点击恢复默认模板
/*
// Definition for a QuadTree node.
class Node {
public:
bool val;
bool isLeaf;
Node* topLeft;
Node* topRight;
Node* bottomLeft;
Node* bottomRight;
Node() {
val = false;
isLeaf = false;
topLeft = NULL;
topRight = NULL;
bottomLeft = NULL;
bottomRight = NULL;
}
Node(bool _val, bool _isLeaf) {
val = _val;
isLeaf = _isLeaf;
topLeft = NULL;
topRight = NULL;
bottomLeft = NULL;
bottomRight = NULL;
}
Node(bool _val, bool _isLeaf, Node* _topLeft, Node* _topRight, Node* _bottomLeft, Node* _bottomRight) {
val = _val;
isLeaf = _isLeaf;
topLeft = _topLeft;
topRight = _topRight;
bottomLeft = _bottomLeft;
bottomRight = _bottomRight;
}
};
*/
class Solution {
public:
Node* intersect(Node* quadTree1, Node* quadTree2) {
}
};
java 解法, 执行用时: 0 ms, 内存消耗: 41.8 MB, 提交时间: 2022-11-29 12:13:29
/*
// Definition for a QuadTree node.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
public Node() {}
public Node(boolean _val,boolean _isLeaf,Node _topLeft,Node _topRight,Node _bottomLeft,Node _bottomRight) {
val = _val;
isLeaf = _isLeaf;
topLeft = _topLeft;
topRight = _topRight;
bottomLeft = _bottomLeft;
bottomRight = _bottomRight;
}
};
*/
class Solution {
public Node intersect(Node quadTree1, Node quadTree2) {
if (quadTree1.isLeaf) {
if (quadTree1.val) {
return new Node(true, true);
}
return new Node(quadTree2.val, quadTree2.isLeaf, quadTree2.topLeft, quadTree2.topRight, quadTree2.bottomLeft, quadTree2.bottomRight);
}
if (quadTree2.isLeaf) {
return intersect(quadTree2, quadTree1);
}
Node o1 = intersect(quadTree1.topLeft, quadTree2.topLeft);
Node o2 = intersect(quadTree1.topRight, quadTree2.topRight);
Node o3 = intersect(quadTree1.bottomLeft, quadTree2.bottomLeft);
Node o4 = intersect(quadTree1.bottomRight, quadTree2.bottomRight);
if (o1.isLeaf && o2.isLeaf && o3.isLeaf && o4.isLeaf && o1.val == o2.val && o1.val == o3.val && o1.val == o4.val) {
return new Node(o1.val, true);
}
return new Node(false, false, o1, o2, o3, o4);
}
}
javascript 解法, 执行用时: 76 ms, 内存消耗: 46.6 MB, 提交时间: 2022-11-29 12:13:01
/**
* // Definition for a QuadTree node.
* function Node(val,isLeaf,topLeft,topRight,bottomLeft,bottomRight) {
* this.val = val;
* this.isLeaf = isLeaf;
* this.topLeft = topLeft;
* this.topRight = topRight;
* this.bottomLeft = bottomLeft;
* this.bottomRight = bottomRight;
* };
*/
/**
* @param {Node} quadTree1
* @param {Node} quadTree2
* @return {Node}
*/
var intersect = function(quadTree1, quadTree2) {
if (quadTree1.isLeaf) {
if (quadTree1.val) {
return new Node(true, true);
}
return new Node(quadTree2.val, quadTree2.isLeaf, quadTree2.topLeft, quadTree2.topRight, quadTree2.bottomLeft, quadTree2.bottomRight);
}
if (quadTree2.isLeaf) {
return intersect(quadTree2, quadTree1);
}
const o1 = intersect(quadTree1.topLeft, quadTree2.topLeft);
const o2 = intersect(quadTree1.topRight, quadTree2.topRight);
const o3 = intersect(quadTree1.bottomLeft, quadTree2.bottomLeft);
const o4 = intersect(quadTree1.bottomRight, quadTree2.bottomRight);
if (o1.isLeaf && o2.isLeaf && o3.isLeaf && o4.isLeaf && o1.val === o2.val && o1.val === o3.val && o1.val === o4.val) {
return new Node(o1.val, true);
}
return new Node(false, false, o1, o2, o3, o4);
};
golang 解法, 执行用时: 8 ms, 内存消耗: 6.5 MB, 提交时间: 2022-11-29 12:12:42
/**
* Definition for a QuadTree node.
* type Node struct {
* Val bool
* IsLeaf bool
* TopLeft *Node
* TopRight *Node
* BottomLeft *Node
* BottomRight *Node
* }
*/
func intersect(quadTree1, quadTree2 *Node) *Node {
if quadTree1.IsLeaf {
if quadTree1.Val {
return &Node{Val: true, IsLeaf: true}
}
return quadTree2
}
if quadTree2.IsLeaf {
return intersect(quadTree2, quadTree1)
}
o1 := intersect(quadTree1.TopLeft, quadTree2.TopLeft)
o2 := intersect(quadTree1.TopRight, quadTree2.TopRight)
o3 := intersect(quadTree1.BottomLeft, quadTree2.BottomLeft)
o4 := intersect(quadTree1.BottomRight, quadTree2.BottomRight)
if o1.IsLeaf && o2.IsLeaf && o3.IsLeaf && o4.IsLeaf && o1.Val == o2.Val && o1.Val == o3.Val && o1.Val == o4.Val {
return &Node{Val: o1.Val, IsLeaf: true}
}
return &Node{false, false, o1, o2, o3, o4}
}
python3 解法, 执行用时: 72 ms, 内存消耗: 15.4 MB, 提交时间: 2022-11-29 12:12:25
"""
# Definition for a QuadTree node.
class Node:
def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):
self.val = val
self.isLeaf = isLeaf
self.topLeft = topLeft
self.topRight = topRight
self.bottomLeft = bottomLeft
self.bottomRight = bottomRight
"""
class Solution:
def intersect(self, quadTree1: 'Node', quadTree2: 'Node') -> 'Node':
if quadTree1.isLeaf:
return Node(True, True) if quadTree1.val else quadTree2
if quadTree2.isLeaf:
return self.intersect(quadTree2, quadTree1)
o1 = self.intersect(quadTree1.topLeft, quadTree2.topLeft)
o2 = self.intersect(quadTree1.topRight, quadTree2.topRight)
o3 = self.intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)
o4 = self.intersect(quadTree1.bottomRight, quadTree2.bottomRight)
if o1.isLeaf and o2.isLeaf and o3.isLeaf and o4.isLeaf and o1.val == o2.val == o3.val == o4.val:
return Node(o1.val, True)
return Node(False, False, o1, o2, o3, o4)