骑士拨号器

935. 骑士拨号器

象棋骑士有一个独特的移动方式，它可以垂直移动两个方格，水平移动一个方格，或者水平移动两个方格，垂直移动一个方格(两者都形成一个 L 的形状)。

象棋骑士可能的移动方式如下图所示:

我们有一个象棋骑士和一个电话垫，如下所示，骑士只能站在一个数字单元格上(即蓝色单元格)。

给定一个整数 n，返回我们可以拨多少个长度为 n 的不同电话号码。

你可以将骑士放置在任何数字单元格上，然后你应该执行 n - 1 次移动来获得长度为 n 的号码。所有的跳跃应该是有效的骑士跳跃。

因为答案可能很大，所以输出答案模 10⁹ + 7.

示例 1：

输入：n = 1
输出：10
解释：我们需要拨一个长度为1的数字，所以把骑士放在10个单元格中的任何一个数字单元格上都能满足条件。

示例 2：

输入：n = 2
输出：20
解释：我们可以拨打的所有有效号码为[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

示例 3：

输入：n = 3131
输出：136006598
解释：注意取模

提示：

1 <= n <= 5000

原站题解

去查看

上次编辑到这里，代码来自缓存点击恢复默认模板

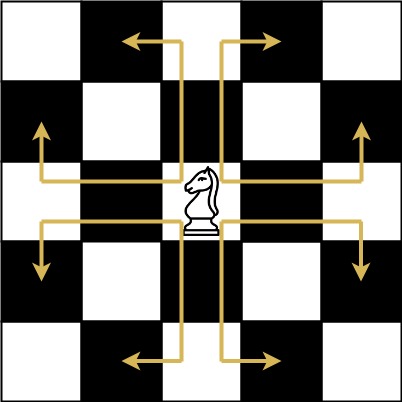
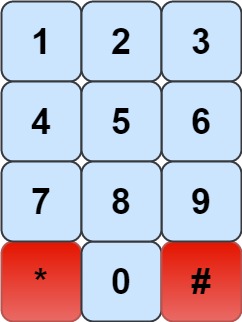
class Solution { public: int knightDialer(int n) { } };

golang 解法, 执行用时: 4 ms, 内存消耗: 1.8 MB, 提交时间: 2023-05-30 09:53:40

func knightDialer(n int) int {
	b1, b2, b3, b4, b5 := 4, 2, 2, 1, 1
	for i := 1; i < n; i++ {
		b1, b2, b3, b4, b5 = (2*b2+2*b3)%1000000007, b1, (b1 + 2*b4)%1000000007, b3, 0
	}
	return (b1 + b2 + b3 + b4 + b5) % 1000000007
}

golang 解法, 执行用时: 20 ms, 内存消耗: 7.1 MB, 提交时间: 2023-05-30 09:53:12

var edge = [][]int{{6, 4}, {8, 6}, {7, 9}, {4, 8}, {0, 3, 9}, {}, {0, 1, 7}, {2, 6}, {1, 3}, {2, 4}}

func knightDialer(n int) int {
	dp := make([][]int, n+1)  // dp[i][j] 长度为i时终点在j上的路径条数
	for i := range dp {
		dp[i] = make([]int, 10)
	}
	for j := range dp[1] {
		dp[1][j] = 1
	}
	for i := 2; i <= n; i++ {
		for j := range dp[i] {
			for _, e := range edge[j] {
				dp[i][j] = (dp[i][j] + dp[i-1][e]) % (1e9 + 7)
			}
		}
	}
	res := 0
	for j := range dp[n] {
		res = (res + dp[n][j]) % (1e9 + 7)
	}
	return res
}

python3 解法, 执行用时: 200 ms, 内存消耗: 16.2 MB, 提交时间: 2023-05-30 09:51:28

class Solution:
    def knightDialer(self, n: int) -> int:
        if n == 1: return 10
        #分别为状态A,B,C,D
        nums = [1,1,1,1]
        for _ in range(0, n-1):
            nums = [nums[1]+nums[2], 2*nums[0], 2*nums[0]+nums[3], 2*nums[2]]
        #状态A有4个数字，B有2个数字，C有2个数字，D有1个数字
        return (4*nums[0]+2*nums[1]+2*nums[2]+nums[3]) % 1000000007

python3 解法, 执行用时: 808 ms, 内存消耗: 15.9 MB, 提交时间: 2023-05-30 09:50:33

class Solution:
    def knightDialer(self, n: int) -> int:
        MOD = 10**9 + 7
        moves = [[4,6],[6,8],[7,9],[4,8],[3,9,0],[],
                     [1,7,0],[2,6],[1,3],[2,4]]

        dp = [1] * 10
        for hops in range(0, n-1):
            dp2 = [0] * 10
            for node, count in enumerate(dp):
                for nei in moves[node]:
                    dp2[nei] += count
                    dp2[nei] %= MOD
            dp = dp2
        return sum(dp) % MOD

java 解法, 执行用时: 19 ms, 内存消耗: 38.2 MB, 提交时间: 2023-05-30 09:49:57

class Solution {
    public int knightDialer(int N) {
        int MOD = 1_000_000_007;
        int[][] moves = new int[][]{
            {4,6},{6,8},{7,9},{4,8},{3,9,0},
            {},{1,7,0},{2,6},{1,3},{2,4}};

        int[][] dp = new int[2][10];
        Arrays.fill(dp[0], 1);
        for (int hops = 0; hops < N-1; ++hops) {
            Arrays.fill(dp[~hops & 1], 0);
            for (int node = 0; node < 10; ++node)
                for (int nei: moves[node]) {
                    dp[~hops & 1][nei] += dp[hops & 1][node];
                    dp[~hops & 1][nei] %= MOD;
                }
        }

        long ans = 0;
        for (int x: dp[~N & 1])
            ans += x;
        return (int) (ans % MOD);
    }
}

上一题

下一题

详情