class Solution {
public:
int minimumSum(vector<vector<int>>& grid) {
}
};
100332. 包含所有 1 的最小矩形面积 II
给你一个二维 二进制 数组 grid。你需要找到 3 个 不重叠、面积 非零 、边在水平方向和竖直方向上的矩形,并且满足 grid 中所有的 1 都在这些矩形的内部。
返回这些矩形面积之和的 最小 可能值。
注意,这些矩形可以相接。
示例 1:
输入: grid = [[1,0,1],[1,1,1]]
输出: 5
解释:
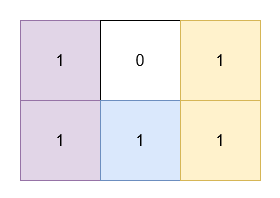
(0, 0) 和 (1, 0) 的 1 被一个面积为 2 的矩形覆盖。(0, 2) 和 (1, 2) 的 1 被一个面积为 2 的矩形覆盖。(1, 1) 的 1 被一个面积为 1 的矩形覆盖。示例 2:
输入: grid = [[1,0,1,0],[0,1,0,1]]
输出: 5
解释:
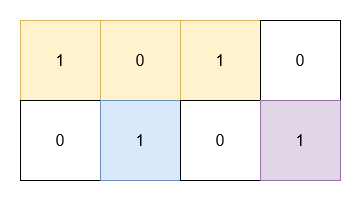
(0, 0) 和 (0, 2) 的 1 被一个面积为 3 的矩形覆盖。(1, 1) 的 1 被一个面积为 1 的矩形覆盖。(1, 3) 的 1 被一个面积为 1 的矩形覆盖。
提示:
1 <= grid.length, grid[i].length <= 30grid[i][j] 是 0 或 1。grid 中至少有三个 1 。相似题目
原站题解
cpp 解法, 执行用时: 48 ms, 内存消耗: 45.4 MB, 提交时间: 2024-06-28 17:52:42
class Solution {// 顺时针旋转矩阵 90°vector<vector<int>> rotate(vector<vector<int>> a) {int m = a.size(), n = a[0].size();vector<vector<int>> b(n, vector<int>(m));for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {b[j][m - 1 - i] = a[i][j];}}return b;}vector<vector<int>> minimumArea(vector<vector<int>>& a) {int m = a.size(), n = a[0].size();// f[i+1][j+1] 表示包含【左上角为 (0,0) 右下角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积vector<vector<int>> f(m + 1, vector<int>(n + 1));vector<tuple<int, int, int>> border(n + 1, {-1, -1, -1});for (int i = 0; i < m; i++) {int left = -1, right = 0;for (int j = 0; j < n; j++) {if (a[i][j]) {if (left < 0) {left = j;}right = j;}auto& [pre_top, pre_left, pre_right] = border[j];if (left < 0) { // 这一排目前全是 0f[i + 1][j + 1] = f[i][j + 1]; // 等于上面的结果} else if (pre_top < 0) { // 这一排有 1,上面全是 0f[i + 1][j + 1] = right - left + 1;border[j] = {i, left, right};} else { // 这一排有 1,上面也有 1int l = min(pre_left, left), r = max(pre_right, right);f[i + 1][j + 1] = (r - l + 1) * (i - pre_top + 1);border[j] = {pre_top, l, r};}}}return f;}int f(vector<vector<int>>& a) {int m = a.size(), n = a[0].size();vector<pair<int, int>> lr(m); // 每一行最左最右 1 的列号for (int i = 0; i < m; i++) {int l = -1, r = 0;for (int j = 0; j < n; j++) {if (a[i][j] > 0) {if (l < 0) {l = j;}r = j;}}lr[i] = {l, r};}// lt[i+1][j+1] = 包含【左上角为 (0,0) 右下角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积vector<vector<int>> lt = minimumArea(a);a = rotate(a);// lb[i][j+1] = 包含【左下角为 (m-1,0) 右上角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积vector<vector<int>> lb = rotate(rotate(rotate(minimumArea(a))));a = rotate(a);// rb[i][j] = 包含【右下角为 (m-1,n-1) 左上角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积vector<vector<int>> rb = rotate(rotate(minimumArea(a)));a = rotate(a);// rt[i+1][j] = 包含【右上角为 (0,n-1) 左下角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积vector<vector<int>> rt = rotate(minimumArea(a));int ans = INT_MAX;if (m >= 3) {for (int i = 1; i < m; i++) {int left = n, right = 0, top = m, bottom = 0;for (int j = i + 1; j < m; j++) {if (auto& [l, r] = lr[j - 1]; l >= 0) {left = min(left, l);right = max(right, r);top = min(top, j - 1);bottom = j - 1;}// 图片上左ans = min(ans, lt[i][n] + (right - left + 1) * (bottom - top + 1) + lb[j][n]);}}}if (m >= 2 && n >= 2) {for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {// 图片上中ans = min(ans, lt[i][n] + lb[i][j] + rb[i][j]);// 图片上右ans = min(ans, lt[i][j] + rt[i][j] + lb[i][n]);}}}return ans;}public:int minimumSum(vector<vector<int>>& grid) {auto g = rotate(grid);return min(f(grid), f(g));}};
java 解法, 执行用时: 11 ms, 内存消耗: 44 MB, 提交时间: 2024-06-28 17:52:29
class Solution {public int minimumSum(int[][] grid) {return Math.min(f(grid), f(rotate(grid)));}private int f(int[][] a) {int m = a.length;int n = a[0].length;int[][] lr = new int[m][2]; // 每一行最左最右 1 的列号for (int i = 0; i < m; i++) {int l = -1;int r = 0;for (int j = 0; j < n; j++) {if (a[i][j] > 0) {if (l < 0) {l = j;}r = j;}}lr[i][0] = l;lr[i][1] = r;}// lt[i+1][j+1] = 包含【左上角为 (0,0) 右下角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积int[][] lt = minimumArea(a);a = rotate(a);// lb[i][j+1] = 包含【左下角为 (m-1,0) 右上角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积int[][] lb = rotate(rotate(rotate(minimumArea(a))));a = rotate(a);// rb[i][j] = 包含【右下角为 (m-1,n-1) 左上角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积int[][] rb = rotate(rotate(minimumArea(a)));a = rotate(a);// rt[i+1][j] = 包含【右上角为 (0,n-1) 左下角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积int[][] rt = rotate(minimumArea(a));int ans = Integer.MAX_VALUE;if (m >= 3) {for (int i = 1; i < m; i++) {int left = n;int right = 0;int top = m;int bottom = 0;for (int j = i + 1; j < m; j++) {int l = lr[j - 1][0];if (l >= 0) {left = Math.min(left, l);right = Math.max(right, lr[j - 1][1]);top = Math.min(top, j - 1);bottom = j - 1;}// 图片上左ans = Math.min(ans, lt[i][n] + (right - left + 1) * (bottom - top + 1) + lb[j][n]);}}}if (m >= 2 && n >= 2) {for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {// 图片上中ans = Math.min(ans, lt[i][n] + lb[i][j] + rb[i][j]);// 图片上右ans = Math.min(ans, lt[i][j] + rt[i][j] + lb[i][n]);}}}return ans;}private int[][] minimumArea(int[][] a) {int m = a.length;int n = a[0].length;// f[i+1][j+1] 表示包含【左上角为 (0,0) 右下角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积int[][] f = new int[m + 1][n + 1];int[][] border = new int[n][3];for (int j = 0; j < n; j++) {border[j][0] = -1;}for (int i = 0; i < m; i++) {int left = -1;int right = 0;for (int j = 0; j < n; j++) {if (a[i][j] == 1) {if (left < 0) {left = j;}right = j;}int[] preB = border[j];if (left < 0) { // 这一排目前全是 0f[i + 1][j + 1] = f[i][j + 1]; // 等于上面的结果} else if (preB[0] < 0) { // 这一排有 1,上面全是 0f[i + 1][j + 1] = right - left + 1;border[j][0] = i;border[j][1] = left;border[j][2] = right;} else { // 这一排有 1,上面也有 1int l = Math.min(preB[1], left);int r = Math.max(preB[2], right);f[i + 1][j + 1] = (r - l + 1) * (i - preB[0] + 1);border[j][1] = l;border[j][2] = r;}}}return f;}// 顺时针旋转矩阵 90°private int[][] rotate(int[][] a) {int m = a.length;int n = a[0].length;int[][] b = new int[n][m];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {b[j][m - 1 - i] = a[i][j];}}return b;}}
golang 解法, 执行用时: 17 ms, 内存消耗: 7 MB, 提交时间: 2024-06-28 17:52:13
func minimumArea(a [][]int) [][]int {m, n := len(a), len(a[0])// f[i+1][j+1] 表示包含【左上角为 (0,0) 右下角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积f := make([][]int, m+1)for i := range f {f[i] = make([]int, n+1)}type data struct{ top, left, right int }border := make([]data, n)for j := range border {border[j].top = -1 // 无}for i, row := range a {left, right := -1, 0for j, x := range row {if x > 0 {if left < 0 {left = j}right = j}preB := border[j]if left < 0 { // 这一排目前全是 0f[i+1][j+1] = f[i][j+1] // 等于上面的结果} else if preB.top < 0 { // 这一排有 1,上面全是 0f[i+1][j+1] = right - left + 1border[j] = data{i, left, right}} else { // 这一排有 1,上面也有 1l, r := min(preB.left, left), max(preB.right, right)f[i+1][j+1] = (r - l + 1) * (i - preB.top + 1)border[j] = data{preB.top, l, r}}}}return f}func minimumSum(grid [][]int) int {ans := math.MaxIntf := func(a [][]int) {m, n := len(a), len(a[0])type pair struct{ l, r int }lr := make([]pair, m) // 每一行最左最右 1 的列号for i, row := range a {l, r := -1, 0for j, x := range row {if x > 0 {if l < 0 {l = j}r = j}}lr[i] = pair{l, r}}// lt[i+1][j+1] = 包含【左上角为 (0,0) 右下角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积lt := minimumArea(a)a = rotate(a)// lb[i][j+1] = 包含【左下角为 (m-1,0) 右上角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积lb := rotate(rotate(rotate(minimumArea(a))))a = rotate(a)// rb[i][j] = 包含【右下角为 (m-1,n-1) 左上角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积rb := rotate(rotate(minimumArea(a)))a = rotate(a)// rt[i+1][j] = 包含【右上角为 (0,n-1) 左下角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积rt := rotate(minimumArea(a))if m >= 3 {for i := 1; i < m; i++ {left, right, top, bottom := n, 0, m, 0for j := i + 1; j < m; j++ {if p := lr[j-1]; p.l >= 0 {left = min(left, p.l)right = max(right, p.r)top = min(top, j-1)bottom = j - 1}// 图片上左area := lt[i][n] // minimumArea(a[:i], 0, n)area += (right - left + 1) * (bottom - top + 1) // minimumArea(a[i:j], 0, n)area += lb[j][n] // minimumArea(a[j:], 0, n)ans = min(ans, area)}}}if m >= 2 && n >= 2 {for i := 1; i < m; i++ {for j := 1; j < n; j++ {// 图片上中area := lt[i][n] // minimumArea(a[:i], 0, n)area += lb[i][j] // minimumArea(a[i:], 0, j)area += rb[i][j] // minimumArea(a[i:], j, n)ans = min(ans, area)// 图片上右area = lt[i][j] // minimumArea(a[:i], 0, j)area += rt[i][j] // minimumArea(a[:i], j, n)area += lb[i][n] // minimumArea(a[i:], 0, n)ans = min(ans, area)}}}}f(grid)f(rotate(grid))return ans}// 顺时针旋转矩阵 90°func rotate(a [][]int) [][]int {m, n := len(a), len(a[0])b := make([][]int, n)for i := range b {b[i] = make([]int, m)}for i, row := range a {for j, x := range row {b[j][m-1-i] = x}}return b}
python3 解法, 执行用时: 135 ms, 内存消耗: 16.7 MB, 提交时间: 2024-06-28 17:51:50
# dp处理class Solution:def minimumSum(self, grid: List[List[int]]) -> int:return min(self.f(grid), self.f(rotate(grid)))def f(self, a: List[List[int]]) -> int:m, n = len(a), len(a[0])lr = [] # 每一行最左最右 1 的列号for i in range(m):l, r = -1, 0for j in range(n):if a[i][j] > 0:if l < 0:l = jr = jlr.append((l, r))def minimumArea(a: List[List[int]]) -> List[List[int]]:m, n = len(a), len(a[0])# f[i+1][j+1] 表示包含【左上角为 (0,0) 右下角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积f = [[0] * (n + 1) for _ in range(m + 1)]border = [(-1, 0, 0)] * nfor i, row in enumerate(a):left, right = -1, 0for j, x in enumerate(row):if x:if left < 0:left = jright = jpre_top, pre_left, pre_right = border[j]if left < 0: # 这一排目前全是 0f[i + 1][j + 1] = f[i][j + 1] # 等于上面的结果elif pre_top < 0: # 这一排有 1,上面全是 0f[i + 1][j + 1] = right - left + 1border[j] = (i, left, right)else: # 这一排有 1,上面也有 1l = min(pre_left, left)r = max(pre_right, right)f[i + 1][j + 1] = (r - l + 1) * (i - pre_top + 1)border[j] = (pre_top, l, r)return f# lt[i+1][j+1] = 包含【左上角为 (0,0) 右下角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积lt = minimumArea(a)a = rotate(a)# lb[i][j+1] = 包含【左下角为 (m-1,0) 右上角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积lb = rotate(rotate(rotate(minimumArea(a))))a = rotate(a)# rb[i][j] = 包含【右下角为 (m-1,n-1) 左上角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积rb = rotate(rotate(minimumArea(a)))a = rotate(a)# rt[i+1][j] = 包含【右上角为 (0,n-1) 左下角为 (i,j) 的子矩形】中的所有 1 的最小矩形面积rt = rotate(minimumArea(a))ans = infif m >= 3:for i in range(1, m):left, right, top, bottom = n, 0, m, 0for j in range(i + 1, m):l, r = lr[j - 1]if l >= 0:left = min(left, l)right = max(right, r)top = min(top, j - 1)bottom = j - 1# 图片上左ans = min(ans, lt[i][n] + (right - left + 1) * (bottom - top + 1) + lb[j][n])if m >= 2 and n >= 2:for i in range(1, m):for j in range(1, n):# 图片上中ans = min(ans, lt[i][n] + lb[i][j] + rb[i][j])# 图片上右ans = min(ans, lt[i][j] + rt[i][j] + lb[i][n])return ans# 顺时针旋转矩阵 90°def rotate(a: List[List[int]]) -> List[List[int]]:return list(zip(*reversed(a)))
golang 解法, 执行用时: 96 ms, 内存消耗: 3.8 MB, 提交时间: 2024-06-28 17:51:10
func minimumArea(a [][]int, l, r int) int {left, right := len(a[0]), 0top, bottom := len(a), 0for i, row := range a {for j, x := range row[l:r] {if x == 1 {left = min(left, j)right = max(right, j)top = min(top, i)bottom = i}}}return (right - left + 1) * (bottom - top + 1)}func minimumSum(grid [][]int) int {ans := math.MaxIntf := func(a [][]int) {m, n := len(a), len(a[0])if m >= 3 {for i := 1; i < m; i++ {for j := i + 1; j < m; j++ {// 图片上左area := minimumArea(a[:i], 0, n)area += minimumArea(a[i:j], 0, n)area += minimumArea(a[j:], 0, n)ans = min(ans, area)}}}if m >= 2 && n >= 2 {for i := 1; i < m; i++ {for j := 1; j < n; j++ {// 图片上中area := minimumArea(a[:i], 0, n)area += minimumArea(a[i:], 0, j)area += minimumArea(a[i:], j, n)ans = min(ans, area)// 图片上右area = minimumArea(a[:i], 0, j)area += minimumArea(a[:i], j, n)area += minimumArea(a[i:], 0, n)ans = min(ans, area)}}}}f(grid)f(rotate(grid))return ans}// 顺时针旋转矩阵 90°func rotate(a [][]int) [][]int {m, n := len(a), len(a[0])b := make([][]int, n)for i := range b {b[i] = make([]int, m)}for i, row := range a {for j, x := range row {b[j][m-1-i] = x}}return b}
python3 解法, 执行用时: 5901 ms, 内存消耗: 16.8 MB, 提交时间: 2024-06-28 17:50:53
# 六种情况,暴力枚举class Solution:def minimumSum(self, grid: List[List[int]]) -> int:return min(self.f(grid), self.f(self.rotate(grid)))def f(self, a: List[List[int]]) -> int:def minimumArea(a: List[List[int]], l: int, r: int) -> int:left, right = len(a[0]), 0top, bottom = len(a), 0for i, row in enumerate(a):for j, x in enumerate(row[l:r]):if x == 1:left = min(left, j)right = max(right, j)top = min(top, i)bottom = ireturn (right - left + 1) * (bottom - top + 1)ans = infm, n = len(a), len(a[0])if m >= 3:for i in range(1, m):for j in range(i + 1, m):# 图片上左area = minimumArea(a[:i], 0, n)area += minimumArea(a[i:j], 0, n)area += minimumArea(a[j:], 0, n)ans = min(ans, area)if m >= 2 and n >= 2:for i in range(1, m):for j in range(1, n):# 图片上中area = minimumArea(a[:i], 0, n)area += minimumArea(a[i:], 0, j)area += minimumArea(a[i:], j, n)ans = min(ans, area)# 图片上右area = minimumArea(a[:i], 0, j)area += minimumArea(a[:i], j, n)area += minimumArea(a[i:], 0, n)ans = min(ans, area)return ans# 顺时针旋转矩阵 90°def rotate(self, a: List[List[int]]) -> List[List[int]]:return list(zip(*reversed(a)))