2737. 找到最近的标记节点

给定一个正整数 n ，表示一个 索引从 0 开始的有向加权 图的节点数量，以及一个 索引从 0 开始的二维数组 edges ，其中 edges[i] = [ui, vi, wi] 表示从节点 ui 到节点 vi 的一条权重为 wi 的边。

并给定一个节点 s 和一个节点数组 marked ；你的任务是找到从 s 到 marked 中 任何 节点的 最短 距离。

返回一个整数，表示从 s 到 marked 中任何节点的最短距离，如果从 s 到任何标记节点没有路径，则返回 -1 。

示例 1：

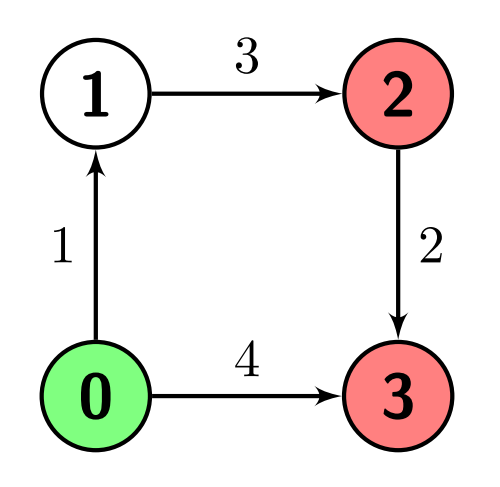
输入：n = 4, edges = [[0,1,1],[1,2,3],[2,3,2],[0,3,4]], s = 0, marked = [2,3]
输出：4
解释：从节点 0（绿色节点）到节点 2（红色节点）有一条路径，即 0->1->2，距离为 1 + 3 = 4。 
从节点 0 到节点 3（红色节点）有两条路径，即 0->1->2->3 和 0->3，分别距离为 1 + 3 + 2 = 6 和 4。 
它们中的最小值是 4。

示例 2：

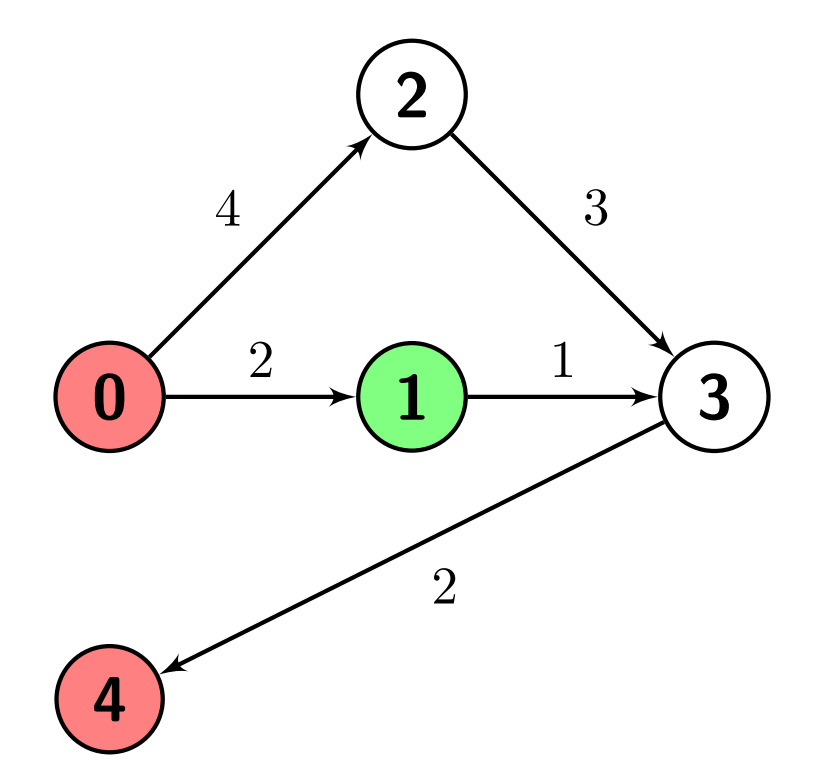
输入：n = 5, edges = [[0,1,2],[0,2,4],[1,3,1],[2,3,3],[3,4,2]], s = 1, marked = [0,4]
输出：3
解释：从节点 1（绿色节点）到节点 0（红色节点）没有路径。 
从节点 1 到节点 4（红色节点）有一条路径，即 1->3->4，距离为 1 + 2 = 3。 
因此答案是 3。

示例 3：

输入：n = 4, edges = [[0,1,1],[1,2,3],[2,3,2]], s = 3, marked = [0,1]
输出：-1
解释：从节点 3（绿色节点）到任何一个标记节点（红色节点）都没有路径，因此答案是 -1。

提示：

• 2 <= n <= 500
• 1 <= edges.length <= 104
• edges[i].length = 3
• 0 <= edges[i][0], edges[i][1] <= n - 1
• 1 <= edges[i][2] <= 106
• 1 <= marked.length <= n - 1
• 0 <= s, marked[i] <= n - 1
• s != marked[i]
• 如果 i != j 则 marked[i] != marked[j]
• 图中可能有 重复的边 。
• 图的生成不会出现 自环 。