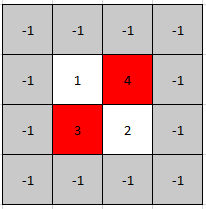
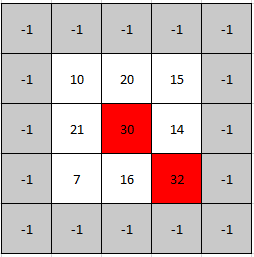
C++
Java
Python
Python3
C
C#
JavaScript
Ruby
Swift
Go
Scala
Kotlin
Rust
PHP
TypeScript
Racket
Erlang
Elixir
Dart
monokai
ambiance
chaos
chrome
cloud9_day
cloud9_night
cloud9_night_low_color
clouds
clouds_midnight
cobalt
crimson_editor
dawn
dracula
dreamweaver
eclipse
github
github_dark
gob
gruvbox
gruvbox_dark_hard
gruvbox_light_hard
idle_fingers
iplastic
katzenmilch
kr_theme
kuroir
merbivore
merbivore_soft
mono_industrial
nord_dark
one_dark
pastel_on_dark
solarized_dark
solarized_light
sqlserver
terminal
textmate
tomorrow
tomorrow_night
tomorrow_night_blue
tomorrow_night_bright
tomorrow_night_eighties
twilight
vibrant_ink
xcode
上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
vector<int> findPeakGrid(vector<vector<int>>& mat) {
}
};
运行代码
提交
golang 解法, 执行用时: 140 ms, 内存消耗: 9.1 MB, 提交时间: 2023-12-19 07:44:41
func maxElement(row []int) int {
i := 0
for j := range row {
if row[i] < row[j] {
i = j
}
}
return i
}
func findPeakGrid(mat [][]int) []int {
m := len(mat)
low, high := 0, m - 1
for low <= high {
i := (low + high) / 2
j := maxElement(mat[i])
if i - 1 >= 0 && mat[i][j] < mat[i - 1][j] {
high = i - 1
continue
}
if i + 1 < m && mat[i][j] < mat[i + 1][j] {
low = i + 1
continue
}
return []int{i, j}
}
return nil // impossible
}
cpp 解法, 执行用时: 144 ms, 内存消耗: 45.6 MB, 提交时间: 2023-12-19 07:44:03
class Solution {
public:
vector<int> findPeakGrid(vector<vector<int>>& mat) {
int m = mat.size(),n = mat[0].size();
int up = 0, down= m-1;
while(up <= down){
int mid = (up + down) / 2;
int maxUp = mid == 0 ? -1 : *max_element(mat[mid - 1].begin(), mat[mid - 1].end());
int maxBottom = mid + 1 == m ? -1 : *max_element(mat[mid + 1].begin(), mat[mid + 1].end());
auto it = max_element(mat[mid].begin(), mat[mid].end());
if(*it >= max(maxUp, maxBottom)) {
return {mid, int(it - mat[mid].begin())};
}else if(maxUp >= max(*it, maxBottom)) {
down = mid;
}else{
up = mid + 1;
}
}
return {};
}
};
python3 解法, 执行用时: 68 ms, 内存消耗: 36.1 MB, 提交时间: 2022-12-05 18:30:48
class Solution:
def findPeakGrid(self, mat: List[List[int]]) -> List[int]:
l, r = 0, len(mat) - 1 # 行
while l <= r:
m = (l + r) >> 1
localMax = max(mat[m]) # 改行最大值
localCol = mat[m].index(localMax) # 对应索引
if m + 1 < len(mat) and mat[m + 1][localCol] > localMax: # 下面更大 则说明下方存在极大值
l = m + 1
elif m - 1 >= 0 and mat[m - 1][localCol] > localMax: # 上面更大 则说明上方存在极大值
r = m - 1
else: # 本身更大 他就是极大值
return [m, localCol]
java 解法, 执行用时: 0 ms, 内存消耗: 78.6 MB, 提交时间: 2022-12-05 18:29:58
class Solution {
public int[] findPeakGrid(int[][] mat) {
int m = mat.length, n = mat[0].length;
int low = 0, high = m - 1, maxIndex = 0;
while (low < high) {
int mid = low + (high - low) / 2;
maxIndex = getMaxIndex(mat[mid]);
if (mat[mid][maxIndex] > mat[mid + 1][maxIndex]) {
high = mid;
} else {
low = mid + 1;
}
}
maxIndex = getMaxIndex(mat[low]);
return new int[]{low, maxIndex};
}
public int getMaxIndex(int[] row) {
int index = 0, maxNum = 0;
int n = row.length;
for (int i = 0; i < n; i++) {
if (row[i] > maxNum) {
maxNum = row[i];
index = i;
}
}
return index;
}
}
java 解法, 执行用时: 0 ms, 内存消耗: 78.3 MB, 提交时间: 2022-12-05 18:29:16
class Solution {
// 返回行最大值的列号
public int maxOfRow(int[][] mat, int row) {
if (row < 0 || row >= mat.length) {
return -1;
}
int col = 0;
for (int i = 1; i < mat[row].length; i++) {
if (mat[row][i] > mat[row][col]) {
col = i;
}
}
return col;
}
public int[] findPeakGrid(int[][] mat) {
int top = 0;
int down = mat.length - 1;
int mid;
// m1 mid前一行最大值列号,m2:mid最大值列号,m3:mid+1行最大值列号
int m1, m2, m3;
int v1, v2, v3; //中间三行对应的最大值
while (top <= down) {
mid = (top + down) / 2;
//System.out.printf("%d %d %d\n",top,mid,down);
m2 = maxOfRow(mat, mid);
if (top == down) {
return new int[]{mid, m2};
}
m1 = maxOfRow(mat, mid - 1);
m3 = maxOfRow(mat, mid + 1);
v1 = mid - 1 >= 0 ? mat[mid - 1][m1] : -1;
v2 = mat[mid][m2];
v3 = mid + 1 < mat.length ? mat[mid + 1][m3] : -1;
// 中间行最大,直接顶峰
if (v2 > v3 && v2 > v1) {
return new int[]{mid, m2};
}
// mid-1行最大
if (v1 > v3 && v1 >= v2) {
down = mid - 1;
} else {
// mid+1行最大
top = mid + 1;
}
}
return null;
}
}
php 解法, 执行用时: 360 ms, 内存消耗: 44.9 MB, 提交时间: 2022-12-05 18:28:27
class Solution {
/**
* @param Integer[][] $mat
* @return Integer[]
*/
function findPeakGrid($mat) {
// 什么样的元素可以成为顶峰元素呢
// 如果一个元素是此行的最大元素,且大于等于上下两行的最大元素,就是一个顶峰元素
// 所以就是相当于对于每行的最大值构成的数组,找一个弱化的顶峰元素
// 一维数组找弱化顶峰元素怎么找呢
// 一个数组里的元素总是上升,下降交替进行的
// 对于一个元素,如果它不小于左右两边,则就是它
// 否则,如果同时小于左右两边,则左右各有一个顶峰
// 若小于左边,大于等于右边,则说明现在是下降阶段,左边有一个顶峰
// 若大于等于左边,小于右边,则说明现在是上升阶段,右边有一个顶峰
$n = count($mat);
$low = 0;
$high = $n - 1;
while ($low <= $high) {
$mid = ($low + $high) >> 1;
// 当前行最大值
$nowMax = max($mat[$mid]);
// 上一行最大值
$upMax = $mid > 0 ? max($mat[$mid - 1]) : -1;
// 下一行最大值
$downMax = $mid < $n - 1 ? max($mat[$mid + 1]) : -1;
if ($nowMax >= $upMax) {
if ($nowMax >= $downMax) { // 就是它
foreach ($mat[$mid] as $j => $value) {
if ($value == $nowMax) {
return [$mid, $j];
}
}
} else { // 下面有顶峰,向下方遍历
$low = $mid + 1;
}
} else { // 直接取上方,因为上方肯定有顶峰
$high = $mid - 1;
}
}
}
}
python3 解法, 执行用时: 56 ms, 内存消耗: 36.2 MB, 提交时间: 2022-12-05 18:26:38
class Solution:
def findPeakGrid(self, mat: List[List[int]]) -> List[int]:
m, n = len(mat), len(mat[0])
# 找到单列中最大值和其索引
def getColMax(i: int) -> (int, int):
value, index = mat[0][i], 0
for row in range(1, m):
if mat[row][i] > value:
value, index = mat[row][i], row
return value, index
# 二分法切片
left, right = 0, n - 1
while left < right:
mid = left + int((right-left)/2)
max_val, max_idx = getColMax(mid)
if mid == 0: # left = 0, right = 1
if max_val > mat[max_idx][1]:
return [max_idx, 0]
else:
left = 1
else:
if mat[max_idx][mid-1] < max_val and mat[max_idx][mid+1] < max_val:
return [max_idx, mid]
elif mat[max_idx][mid-1] < max_val < mat[max_idx][mid+1]:
left = mid + 1
else:
right = mid - 1
# 对于最后剩下的一列,其最大值一定是极大值
_, idx = getColMax(left)
return [idx, left]