描述绘画结果

1943. 描述绘画结果

给你一个细长的画，用数轴表示。这幅画由若干有重叠的线段表示，每个线段有 独一无二 的颜色。给你二维整数数组 segments ，其中 segments[i] = [start_i, end_i, color_i] 表示线段为 半开区间 [start_i, end_i) 且颜色为 color_i 。

线段间重叠部分的颜色会被混合。如果有两种或者更多颜色混合时，它们会形成一种新的颜色，用一个集合表示这个混合颜色。

比方说，如果颜色 2 ，4 和 6 被混合，那么结果颜色为 {2,4,6} 。

为了简化题目，你不需要输出整个集合，只需要用集合中所有元素的和来表示颜色集合。

你想要用 最少数目 不重叠 半开区间 来表示这幅混合颜色的画。这些线段可以用二维数组 painting 表示，其中 painting[j] = [left_j, right_j, mix_j] 表示一个 半开区间[left_j, right_j) 的颜色和为 mix_j 。

比方说，这幅画由 segments = [[1,4,5],[1,7,7]] 组成，那么它可以表示为 painting = [[1,4,12],[4,7,7]] ，因为：
- [1,4) 由颜色 {5,7} 组成（和为 12），分别来自第一个线段和第二个线段。
- [4,7) 由颜色 {7} 组成，来自第二个线段。

请你返回二维数组 painting ，它表示最终绘画的结果（没有被涂色的部分不出现在结果中）。你可以按 任意顺序 返回最终数组的结果。

半开区间 [a, b) 是数轴上点 a 和点 b 之间的部分，包含点 a 且 不包含 点 b 。

示例 1：

输入：segments = [[1,4,5],[4,7,7],[1,7,9]]
输出：[[1,4,14],[4,7,16]]
解释：绘画借故偶可以表示为：
- [1,4) 颜色为 {5,9} （和为 14），分别来自第一和第二个线段。
- [4,7) 颜色为 {7,9} （和为 16），分别来自第二和第三个线段。

示例 2：

输入：segments = [[1,7,9],[6,8,15],[8,10,7]]
输出：[[1,6,9],[6,7,24],[7,8,15],[8,10,7]]
解释：绘画结果可以以表示为：
- [1,6) 颜色为 9 ，来自第一个线段。
- [6,7) 颜色为 {9,15} （和为 24），来自第一和第二个线段。
- [7,8) 颜色为 15 ，来自第二个线段。
- [8,10) 颜色为 7 ，来自第三个线段。

示例 3：

输入：segments = [[1,4,5],[1,4,7],[4,7,1],[4,7,11]]
输出：[[1,4,12],[4,7,12]]
解释：绘画结果可以表示为：
- [1,4) 颜色为 {5,7} （和为 12），分别来自第一和第二个线段。
- [4,7) 颜色为 {1,11} （和为 12），分别来自第三和第四个线段。
注意，只返回一个单独的线段 [1,7) 是不正确的，因为混合颜色的集合不相同。

提示：

1 <= segments.length <= 2 * 10⁴
segments[i].length == 3
1 <= start_i < end_i <= 10⁵
1 <= color_i <= 10⁹
每种颜色 color_i 互不相同。

原站题解

去查看

上次编辑到这里，代码来自缓存点击恢复默认模板

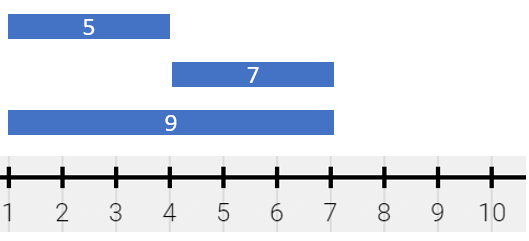
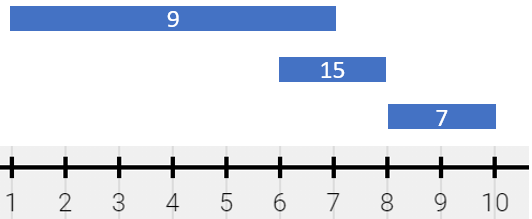
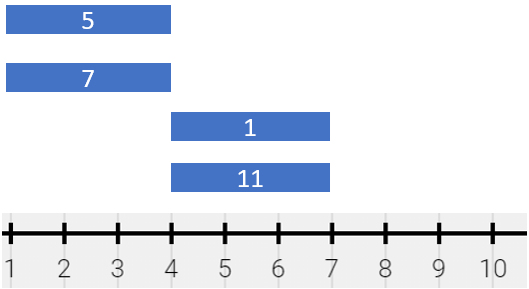
class Solution { public: vector<vector<long long>> splitPainting(vector<vector<int>>& segments) { } };

golang 解法, 执行用时: 220 ms, 内存消耗: 10.8 MB, 提交时间: 2023-09-23 00:42:26

// 由于只有在区间端点处才会改变颜色（增加或减少），可以统计所有区间端点并按位置从小到大排序，
// 然后遍历这些端点，在每个端点处累加颜色并记录答案。
func splitPainting(segments [][]int) (ans [][]int64) {
	type event struct{ pos, color int }
	events := make([]event, 0, len(segments)*2)
	for _, seg := range segments {
		events = append(events, event{seg[0], seg[2]}, event{seg[1], -seg[2]}) // 记录每个区间左右端点及颜色
	}
	sort.Slice(events, func(i, j int) bool { return events[i].pos < events[j].pos }) // 按位置排序

	sum := 0
	for i, e := range events[:len(events)-1] {
		sum += e.color
		if sum > 0 && e.pos < events[i+1].pos {
			ans = append(ans, []int64{int64(e.pos), int64(events[i+1].pos), int64(sum)})
		}
	}
	return
}

java 解法, 执行用时: 141 ms, 内存消耗: 60.4 MB, 提交时间: 2023-09-23 00:41:44

class Solution 
{
    public List<List<Long>> splitPainting(int[][] segments) 
    {
        TreeMap<Integer, Long> i_diff = new TreeMap<>();
        for (int [] s : segments)
        {
            int l = s[0],  r = s[1],  c = s[2];
            i_diff.put(l, i_diff.getOrDefault(l, 0L) + (long)c);
            i_diff.put(r, i_diff.getOrDefault(r, 0L) - (long)c);
        }

        List<List<Long>> res = new ArrayList<>();
        Long last_i = 0L;             //区间的左端点
        Long cur_color = 0L;       //区间的颜色（就是个大数值）
        for (Integer i : i_diff.keySet())
        {
            Long diff = i_diff.get(i);

            if (cur_color != 0)
            {
                List<Long> tmp = new ArrayList<>();
                tmp.add(last_i);
                tmp.add((long)i);
                tmp.add(cur_color);
                res.add(tmp);
            }

            last_i = (long)i;
            cur_color += diff;
        }

        return res;
    }
}

python3 解法, 执行用时: 624 ms, 内存消耗: 38.4 MB, 提交时间: 2023-09-23 00:41:11

from collections import defaultdict

class Solution:
    def splitPainting(self, segments: List[List[int]]) -> List[List[int]]:
        # 计算每个位置对应的颜色和改变量并用哈希表存储
        color = defaultdict(lambda: 0)
        for l, r, c in segments:
            color[l] += c
            color[r] -= c
        # 将哈希表转化为数组并按数轴坐标升序排序
        axis = sorted([[k, v] for k, v in color.items()])
        # 对数组求前缀和计算对应颜色和
        n = len(axis)
        for i in range(1, n):
            axis[i][1] += axis[i-1][1]
        # 遍历数组生成最终绘画结果
        res = []
        for i in range(n - 1):
            if axis[i][1]:
                res.append([axis[i][0], axis[i+1][0], axis[i][1]])
        return res

cpp 解法, 执行用时: 304 ms, 内存消耗: 110.6 MB, 提交时间: 2023-09-23 00:40:57

class Solution {
public:
    vector<vector<long long>> splitPainting(vector<vector<int>>& segments) {
        // 计算每个位置对应的颜色和改变量并用哈希表存储
        unordered_map<int, long long> color;
        for (auto&& segment : segments){
            int l = segment[0];
            int r = segment[1];
            int c = segment[2];
            if (!color.count(l)){
                color[l] = 0;
            }
            color[l] += c;
            if (!color.count(r)){
                color[r] = 0;
            }
            color[r] -= c;
        }
        // 将哈希表转化为数组并按数轴坐标升序排序
        vector<pair<int, long long>> axis;
        for (auto&& [k, v] : color){
            axis.emplace_back(k, v);
        }
        sort(axis.begin(), axis.end());
        // 对数组求前缀和计算对应颜色和
        int n = axis.size();
        for (int i = 1; i < n; ++i){
            axis[i].second += axis[i-1].second;
        }
        // 遍历数组生成最终绘画结果
        vector<vector<long long>> res;
        for (int i = 0; i < n - 1; ++i){
            if (axis[i].second){
                res.emplace_back(vector<long long> {axis[i].first, axis[i+1].first, axis[i].second});
            }
        }
        return res;
    }
};

上一题

下一题

详情