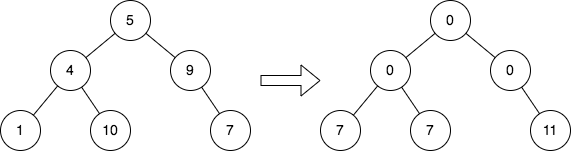
上次编辑到这里,代码来自缓存 点击恢复默认模板
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* replaceValueInTree(TreeNode* root) {
}
};
cpp 解法, 执行用时: 2179 ms, 内存消耗: 280.5 MB, 提交时间: 2024-02-07 09:21:44
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode *replaceValueInTree(TreeNode *root) {
root->val = 0;
vector<TreeNode*> q = {root};
while (!q.empty()) {
vector<TreeNode*> nxt;
// 计算下一层的节点值之和
int next_level_sum = 0;
for (auto node : q) {
if (node->left) {
nxt.push_back(node->left);
next_level_sum += node->left->val;
}
if (node->right) {
nxt.push_back(node->right);
next_level_sum += node->right->val;
}
}
// 再次遍历,更新下一层的节点值
for (auto node : q) {
int children_sum = (node->left ? node->left->val : 0) +
(node->right ? node->right->val : 0);
if (node->left) node->left->val = next_level_sum - children_sum;
if (node->right) node->right->val = next_level_sum - children_sum;
}
q = move(nxt);
}
return root;
}
};
golang 解法, 执行用时: 292 ms, 内存消耗: 23.3 MB, 提交时间: 2023-04-17 17:04:22
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func replaceValueInTree(root *TreeNode) *TreeNode {
root.Val = 0
q := []*TreeNode{root}
for len(q) > 0 {
tmp := q
q = nil
nextLevelSum := 0 // 下一层的节点值之和
for _, node := range tmp {
if node.Left != nil {
q = append(q, node.Left)
nextLevelSum += node.Left.Val
}
if node.Right != nil {
q = append(q, node.Right)
nextLevelSum += node.Right.Val
}
}
// 再次遍历,更新下一层的节点值
for _, node := range tmp {
childrenSum := 0 // node 左右儿子的节点值之和
if node.Left != nil {
childrenSum += node.Left.Val
}
if node.Right != nil {
childrenSum += node.Right.Val
}
// 更新 node 左右儿子的节点值
if node.Left != nil {
node.Left.Val = nextLevelSum - childrenSum
}
if node.Right != nil {
node.Right.Val = nextLevelSum - childrenSum
}
}
}
return root
}
java 解法, 执行用时: 19 ms, 内存消耗: 65.8 MB, 提交时间: 2023-04-17 17:04:09
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode replaceValueInTree(TreeNode root) {
root.val = 0;
var q = new ArrayList<TreeNode>();
q.add(root);
while (!q.isEmpty()) {
var tmp = q;
q = new ArrayList<>();
int nextLevelSum = 0; // 下一层的节点值之和
for (var node : tmp) {
if (node.left != null) {
q.add(node.left);
nextLevelSum += node.left.val;
}
if (node.right != null) {
q.add(node.right);
nextLevelSum += node.right.val;
}
}
// 再次遍历,更新下一层的节点值
for (var node : tmp) {
int childrenSum = (node.left != null ? node.left.val : 0) +
(node.right != null ? node.right.val : 0);
if (node.left != null) node.left.val = nextLevelSum - childrenSum;
if (node.right != null) node.right.val = nextLevelSum - childrenSum;
}
}
return root;
}
}
python3 解法, 执行用时: 760 ms, 内存消耗: 64 MB, 提交时间: 2023-04-17 17:03:55
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def replaceValueInTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
root.val = 0
q = [root]
while q:
tmp = q
q = []
next_level_sum = 0 # 下一层的节点值之和
for node in tmp:
if node.left:
q.append(node.left)
next_level_sum += node.left.val
if node.right:
q.append(node.right)
next_level_sum += node.right.val
# 再次遍历,更新下一层的节点值
for node in tmp:
children_sum = (node.left.val if node.left else 0) + \
(node.right.val if node.right else 0)
if node.left: node.left.val = next_level_sum - children_sum
if node.right: node.right.val = next_level_sum - children_sum
return root