列表

详情

100359. 统计 X 和 Y 频数相等的子矩阵数量

给你一个二维字符矩阵 grid，其中 grid[i][j] 可能是 'X'、'Y' 或 '.'，返回满足以下条件的子矩阵数量：

 

示例 1：

输入： grid = [["X","Y","."],["Y",".","."]]

输出： 3

解释：

示例 2：

输入： grid = [["X","X"],["X","Y"]]

输出： 0

解释：

不存在满足 'X' 和 'Y' 频数相等的子矩阵。

示例 3：

输入： grid = [[".","."],[".","."]]

输出： 0

解释：

不存在满足至少包含一个 'X' 的子矩阵。

 

提示：

相似题目

最大相等频率

统计全 1 子矩形

原站题解

去查看

上次编辑到这里，代码来自缓存 点击恢复默认模板
class Solution { public: int numberOfSubmatrices(vector<vector<char>>& grid) { } };

php 解法, 执行用时: 1093 ms, 内存消耗: 129.3 MB, 提交时间: 2024-07-09 10:12:08 

class Solution {

    /**
     * @param String[][] $grid
     * @return Integer
     */
    function numberOfSubmatrices($grid) {
        $ans = 0;
    	$colCnt = array_fill(0, count($grid[0]), [0, 0]);
    	foreach ( $grid as $row ) {
    		$s0 = 0; 
    		$s1 = 0;
    		foreach  ($row as $j => $c ) {
    			if ( $c != '.' ) {
    				$colCnt[$j][ord($c) & 1]++;
    			}
    			$s0 += $colCnt[$j][0];
    			$s1 += $colCnt[$j][1];
    			if ( $s0 > 0 && $s0 == $s1 ) {
    				$ans++;
    			}
    		}
    	}
    	return $ans;
    }
}

golang 解法, 执行用时: 46 ms, 内存消耗: 12.1 MB, 提交时间: 2024-07-09 10:08:30 

func numberOfSubmatrices(grid [][]byte) (ans int) {
	colCnt := make([][2]int, len(grid[0]))
	for _, row := range grid {
		s0, s1 := 0, 0
		for j, c := range row {
			if c != '.' {
				colCnt[j][c&1]++
			}
			s0 += colCnt[j][0]
			s1 += colCnt[j][1]
			if s0 > 0 && s0 == s1 {
				ans++
			}
		}
	}
	return
}

// 二维前缀和
func numberOfSubmatrices2(grid [][]byte) (ans int) {
	m, n := len(grid), len(grid[0])
	sum := make([][][2]int, m+1)
	for i := range sum {
		sum[i] = make([][2]int, n+1)
	}
	for i, row := range grid {
		for j, c := range row {
			sum[i+1][j+1][0] = sum[i+1][j][0] + sum[i][j+1][0] - sum[i][j][0]
			sum[i+1][j+1][1] = sum[i+1][j][1] + sum[i][j+1][1] - sum[i][j][1]
			if c != '.' {
				sum[i+1][j+1][c&1]++
			}
			if sum[i+1][j+1][0] > 0 && sum[i+1][j+1][0] == sum[i+1][j+1][1] {
				ans++
			}
		}
	}
	return
}

cpp 解法, 执行用时: 471 ms, 内存消耗: 125.6 MB, 提交时间: 2024-07-09 10:07:58 

class Solution {
public:
    int numberOfSubmatrices(vector<vector<char>>& grid) {
        int ans = 0, m = grid.size(), n = grid[0].size();
        vector<vector<array<int, 2>>> sum(m + 1, vector<array<int, 2>>(n + 1));
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                sum[i + 1][j + 1][0] = sum[i + 1][j][0] + sum[i][j + 1][0] - sum[i][j][0];
                sum[i + 1][j + 1][1] = sum[i + 1][j][1] + sum[i][j + 1][1] - sum[i][j][1];
                if (grid[i][j] != '.') {
                    sum[i + 1][j + 1][grid[i][j] & 1]++;
                }
                if (sum[i + 1][j + 1][0] && sum[i + 1][j + 1][0] == sum[i + 1][j + 1][1]) {
                    ans++;
                }
            }
        }
        return ans;
    }

    // 维护每列字符个数
    int numberOfSubmatrices2(vector<vector<char>>& grid) {
        int ans = 0;
        vector<array<int, 2>> col_cnt(grid[0].size());
        for (auto& row : grid) {
            int s0 = 0, s1 = 0;
            for (int j = 0; j < row.size(); j++) {
                if (row[j] != '.') {
                    col_cnt[j][row[j] & 1]++;
                }
                s0 += col_cnt[j][0];
                s1 += col_cnt[j][1];
                if (s0 && s0 == s1) {
                    ans++;
                }
            }
        }
        return ans;
    }
};

java 解法, 执行用时: 13 ms, 内存消耗: 113.8 MB, 提交时间: 2024-07-09 10:07:21 

class Solution {
    public int numberOfSubmatrices(char[][] grid) {
        int ans = 0;
        int[][] colCnt = new int[grid[0].length][2];
        for (char[] row : grid) {
            int s0 = 0, s1 = 0;
            for (int j = 0; j < row.length; j++) {
                if (row[j] != '.') {
                    colCnt[j][row[j] & 1]++;
                }
                s0 += colCnt[j][0];
                s1 += colCnt[j][1];
                if (s0 > 0 && s0 == s1) {
                    ans++;
                }
            }
        }
        return ans;
    }

    // 二维前缀和
    public int numberOfSubmatrices2(char[][] grid) {
        int ans = 0;
        int m = grid.length;
        int n = grid[0].length;
        int[][][] sum = new int[m + 1][n + 1][2];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                sum[i + 1][j + 1][0] = sum[i + 1][j][0] + sum[i][j + 1][0] - sum[i][j][0];
                sum[i + 1][j + 1][1] = sum[i + 1][j][1] + sum[i][j + 1][1] - sum[i][j][1];
                if (grid[i][j] != '.') {
                    sum[i + 1][j + 1][grid[i][j] & 1]++;
                }
                if (sum[i + 1][j + 1][0] > 0 && sum[i + 1][j + 1][0] == sum[i + 1][j + 1][1]) {
                    ans++;
                }
            }
        }
        return ans;
    }
}

python3 解法, 执行用时: 1825 ms, 内存消耗: 238.1 MB, 提交时间: 2024-07-09 10:06:15 

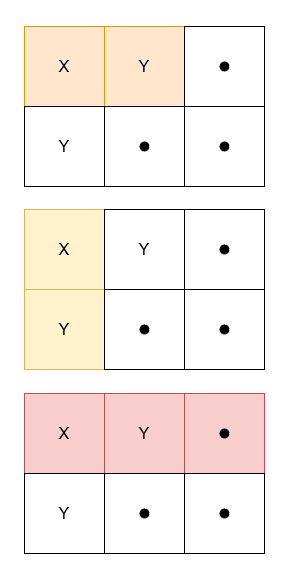
# 方法一：二位前缀和
# 代码实现时，可以取 X 和 Y 的 ASCII 值二进制的最低位，表示 0 和 1。
class Solution:
    def numberOfSubmatrices(self, grid: List[List[str]]) -> int:
        ans = 0
        m, n = len(grid), len(grid[0])
        s = [[[0, 0] for _ in range(n + 1)] for _ in range(m + 1)]
        for i, row in enumerate(grid):
            for j, c in enumerate(row):
                s[i + 1][j + 1][0] = s[i + 1][j][0] + s[i][j + 1][0] - s[i][j][0]
                s[i + 1][j + 1][1] = s[i + 1][j][1] + s[i][j + 1][1] - s[i][j][1]
                if c != '.':
                    s[i + 1][j + 1][ord(c) & 1] += 1
                if s[i + 1][j + 1][0] and s[i + 1][j + 1][0] == s[i + 1][j + 1][1]:
                    ans += 1
        return ans
        
    # 方法二，维护每列字符个数
    def numberOfSubmatrices2(self, grid: List[List[str]]) -> int:
        ans = 0
        col_cnt = [[0, 0] for _ in grid[0]] # 每列x和y的个数
        for row in grid:
            s0 = s1 = 0
            for j, c in enumerate(row):
                if c != '.':
                    col_cnt[j][ord(c) & 1] += 1
                s0 += col_cnt[j][0]
                s1 += col_cnt[j][1]
                if s0 and s0 == s1:
                    ans += 1
        return ans

上一题

© 2024 leetcode.cn