C++
Java
Python
Python3
C
C#
JavaScript
TypeScript
PHP
Swift
Kotlin
Go
Ruby
Scala
monokai
ambiance
chaos
chrome
cloud9_day
cloud9_night
cloud9_night_low_color
clouds
clouds_midnight
cobalt
crimson_editor
dawn
dracula
dreamweaver
eclipse
github
github_dark
gob
gruvbox
gruvbox_dark_hard
gruvbox_light_hard
idle_fingers
iplastic
katzenmilch
kr_theme
kuroir
merbivore
merbivore_soft
mono_industrial
nord_dark
one_dark
pastel_on_dark
solarized_dark
solarized_light
sqlserver
terminal
textmate
tomorrow
tomorrow_night
tomorrow_night_blue
tomorrow_night_bright
tomorrow_night_eighties
twilight
vibrant_ink
xcode
上次编辑到这里,代码来自缓存 点击恢复默认模板
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node() {}
Node(int _val) {
val = _val;
left = NULL;
right = NULL;
}
Node(int _val, Node* _left, Node* _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
class Solution {
public:
Node* treeToDoublyList(Node* root) {
}
};
运行代码
提交
cpp 解法, 执行用时: 8 ms, 内存消耗: 7.7 MB, 提交时间: 2023-10-17 17:50:45
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node() {}
Node(int _val) {
val = _val;
left = NULL;
right = NULL;
}
Node(int _val, Node* _left, Node* _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
class Solution {
Node *currNode;
public:
Node* treeToDoublyList(Node* root) {
Node dummyHead(0, 0, root);
currNode = &dummyHead;
if(root) {
inOrdTra(root);
currNode->right = dummyHead.right;
dummyHead.right->left = currNode;
}
return dummyHead.right;
}
// 中序遍历
void inOrdTra(Node *t) {
if(t) {
inOrdTra(t->left);
currNode->right = t;
t->left = currNode;
currNode = t;
inOrdTra(t->right);
}
}
};
golang 解法, 执行用时: 0 ms, 内存消耗: 2.7 MB, 提交时间: 2023-10-17 17:49:04
/**
* Definition for a Node.
* type Node struct {
* Val int
* Left *Node
* Right *Node
* }
*/
// 左根右
func treeToDoublyList(root *Node) *Node {
// 前驱节点,当前头节点
var pre, head *Node
stack := []*Node{}
for root != nil || len(stack) > 0 {
// 中序遍历每次都从当前节点的最左孩子开始处理
for root != nil {
stack = append(stack, root)
root = root.Left
}
// 出栈处理当前节点
root = stack[len(stack)-1]
stack = stack[:len(stack)-1]
// 首次遍历,前驱节点为空,则记录头节点
if pre == nil {
head = root
} else {
// 非首次遍历,前驱节点与刚出栈的根节点相互指向建立连接
pre.Right = root
root.Left = pre
}
// 前驱节点记录当前根节点,切换到右孩子进行处理
pre = root
root = root.Right
}
// 单向循环结束以后,需要将最左孩子与最右孩子相互指向建立连接
if pre != nil && head != nil {
pre.Right = head
head.Left = pre
}
return head
}
golang 解法, 执行用时: 4 ms, 内存消耗: 2.8 MB, 提交时间: 2023-10-17 17:48:38
/**
* Definition for a Node.
* type Node struct {
* Val int
* Left *Node
* Right *Node
* }
*/
func treeToDoublyList(root *Node) *Node {
if root==nil{return nil}
first:=&Node{}
last:=first
var dfs func(*Node)
dfs = func(node *Node){
if node==nil{
return
}
dfs(node.Left)
last.Right=node
node.Left=last
last = last.Right
dfs(node.Right)
}
dfs(root)
//构造环
head:=first.Right
head.Left=last
last.Right=head
return head
}
python3 解法, 执行用时: 48 ms, 内存消耗: 17.3 MB, 提交时间: 2023-10-17 17:47:31
"""
# Definition for a Node.
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
"""
class Solution:
# 分治,递归
def treeToDoublyList(self, root: 'Node') -> 'Node':
if not root: return
left = self.treeToDoublyList(root.left)
right = self.treeToDoublyList(root.right)
root.left = root
root.right = root
return self.connect(self.connect(left, root), right)
def connect(self, node1, node2):
if not (node1 and node2):
return node1 or node2
tail1, tail2 = node1.left, node2.left
tail1.right = node2
node2.left = tail1
tail2.right = node1
node1.left = tail2
return node1
python3 解法, 执行用时: 60 ms, 内存消耗: 16.8 MB, 提交时间: 2023-10-17 17:46:36
"""
# Definition for a Node.
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
"""
class Solution:
# 非递归,中序遍历
def treeToDoublyList(self, root: 'Node') -> 'Node':
if not root:return
# 当一个中间节点
head = Node(-1, None, None)
# 记录为先前节点,找到下一个节点才能串起来
prev = head
# 中序遍历的非递归
stack = []
p = root
while p or stack:
while p:
stack.append(p)
p = p.left
p = stack.pop()
# 改变左右方向
prev.right = p
p.left = prev
# 改变先前节点
prev = p
p = p.right
# 将head 删掉
head.right.left = prev
prev.right = head.right
return head.right
# 递归,中序遍历
def treeToDoublyList2(self, root: 'Node') -> 'Node':
if not root:return
# 当一个中间节点
head = Node(-1, None, None)
# 记录为先前节点,找到下一个节点才能串起来
prev = head
# 中序遍历的递归
def inorder(root):
nonlocal prev
if not root:
return
inorder(root.left)
prev.right = root
root.left = prev
prev = prev.right
inorder(root.right)
inorder(root)
# 将head 删掉
head.right.left = prev
prev.right = head.right
return head.right
java 解法, 执行用时: 1 ms, 内存消耗: 39.8 MB, 提交时间: 2023-10-17 17:45:10
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val,Node _left,Node _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
// 迭代版本
class Solution {
Node first;
Node pre;
public Node treeToDoublyList(Node root) {
if (root == null) return null;
Stack<Node> stack = new Stack<>();
do {
while (root != null) {
stack.push(root);
root = root.left;
}
if (!stack.isEmpty()) {
Node node = stack.pop();
//first若为空则赋值,first只赋值一次
if (first == null) {
first = node;
}
//pre为空则赋值
if (pre == null) {
pre = node;
}
//否则将当前节点与pre连接,同时移动pre
else {
pre.right = node;
node.left = pre;
pre = node;
}
root = node.right;
}
} while (!stack.isEmpty() || root != null);
//连接头尾
first.left = pre;
pre.right = first;
return first;
}
}
// 递归版本
class Solution1 {
Node first;
Node pre;
public Node treeToDoublyList(Node root) {
if (root == null) return null;
helper(root);
first.left = pre;
pre.right = first;
return first;
}
public void helper(Node node) {
if (node == null) return;
//中序遍历先访问左子树
helper(node.left);
//访问当前节点
//first若为空则赋值,first只赋值一次
if (first == null) {
first = node;
}
//pre为空则赋值
if (pre == null) {
pre = node;
}
//否则将当前节点与pre连接,同时移动pre
else {
pre.right = node;
node.left = pre;
pre = node;
}
//最后访问右子树
helper(node.right);
}
}
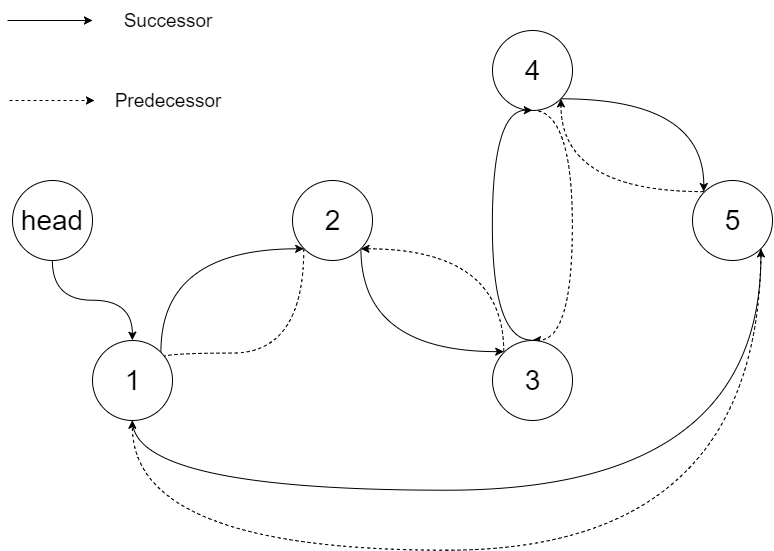
输出:[1,2,3,4,5] 解释:下图显示了转化后的二叉搜索树,实线表示后继关系,虚线表示前驱关系。