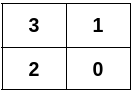
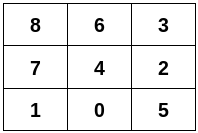
cpp 解法, 执行用时: 314 ms, 内存消耗: 263.2 MB, 提交时间: 2024-10-22 09:26:30

class Solution {
public:
    vector<vector<int>> constructGridLayout(int n, vector<vector<int>>& edges) {
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            int x = e[0], y = e[1];
            g[x].push_back(y);
            g[y].push_back(x);
        }

        // 每种度数选一个点
        int deg_to_node[5]{-1, -1, -1, -1, -1};
        for (int x = 0; x < n; x++) {
            deg_to_node[g[x].size()] = x;
        }

        vector<int> row;
        if (deg_to_node[1] != -1) {
            // 答案只有一列
            row = {deg_to_node[1]};
        } else if (deg_to_node[4] == -1) {
            // 答案只有两列
            int x = deg_to_node[2];
            for (int y : g[x]) {
                if (g[y].size() == 2) {
                    row = {x, y};
                    break;
                }
            }
        } else {
            // 答案至少有三列
            // 寻找度数为 2333...32 的序列作为第一排
            int x = deg_to_node[2];
            row = {x};
            int pre = x;
            x = g[x][0];
            while (g[x].size() == 3) {
                row.push_back(x);
                for (int y : g[x]) {
                    if (y != pre && g[y].size() < 4) {
                        pre = x;
                        x = y;
                        break;
                    }
                }
            }
            row.push_back(x); // x 的度数是 2
        }

        vector<int> vis(n);
        for (int x : row) {
            vis[x] = true;
        }
        vector<vector<int>> ans(n / row.size());
        ans[0] = move(row);
        for (int i = 1; i < ans.size(); i++) {
            for (int x : ans[i - 1]) {
                for (int y : g[x]) {
                    // x 上左右的邻居都访问过了，没访问过的邻居只会在 x 下面
                    if (!vis[y]) {
                        vis[y] = true;
                        ans[i].push_back(y);
                        break;
                    }
                }
            }
        }
        return ans;
    }
};

java 解法, 执行用时: 49 ms, 内存消耗: 100.9 MB, 提交时间: 2024-10-22 09:26:13

class Solution {
    public int[][] constructGridLayout(int n, int[][] edges) {
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (int[] e : edges) {
            int x = e[0];
            int y = e[1];
            g[x].add(y);
            g[y].add(x);
        }

        // 找一个度数最小的点
        int x = 0;
        for (int i = 0; i < g.length; i++) {
            if (g[i].size() < g[x].size()) {
                x = i;
            }
        }

        List<Integer> row = new ArrayList<>();
        row.add(x);
        int degSt = g[x].size(); // 起点的度数
        int pre = -1;
        do { // 注意题目保证 n >= 2，可以至少循环一次
            int nxt = -1;
            for (int y : g[x]) {
                if (y != pre && (nxt < 0 || g[y].size() < g[nxt].size())) {
                    nxt = y;
                }
            }
            pre = x;
            x = nxt;
            row.add(x);
        } while (g[x].size() > degSt);

        int k = row.size();
        int[][] ans = new int[n / k][k];
        boolean[] vis = new boolean[n];
        for (int j = 0; j < k; j++) {
            x = row.get(j);
            ans[0][j] = x;
            vis[x] = true;
        }
        for (int i = 1; i < ans.length; i++) {
            for (int j = 0; j < k; j++) {
                for (int y : g[ans[i - 1][j]]) {
                    // 上左右的邻居都访问过了，没访问过的邻居只会在下面
                    if (!vis[y]) {
                        vis[y] = true;
                        ans[i][j] = y;
                        break;
                    }
                }
            }
        }
        return ans;
    }
}

python3 解法, 执行用时: 192 ms, 内存消耗: 54.5 MB, 提交时间: 2024-10-22 09:25:59

class Solution:
    def constructGridLayout(self, n: int, edges: List[List[int]]) -> List[List[int]]:
        g = [[] for _ in range(n)]
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)

        # 找一个度数最小的点
        x = 0
        for i, to in enumerate(g):
            if len(to) < len(g[x]):
                x = i

        row = [x]
        vis = [False] * n
        vis[x] = True
        deg_st = len(g[x])  # 起点的度数
        while True:  # 注意题目保证 n >= 2，可以至少循环一次
            nxt = -1
            for y in g[x]:
                if not vis[y] and (nxt < 0 or len(g[y]) < len(g[nxt])):
                    nxt = y
            x = nxt
            row.append(x)
            vis[x] = True
            if len(g[x]) == deg_st:
                break

        ans = [[] for _ in range(n // len(row))]
        ans[0] = row
        for i in range(1, len(ans)):
            for x in ans[i - 1]:
                for y in g[x]:
                    # x 上左右的邻居都访问过了，没访问过的邻居只会在 x 下面
                    if not vis[y]:
                        vis[y] = True
                        ans[i].append(y)
                        break
        return ans

golang 解法, 执行用时: 73 ms, 内存消耗: 22.4 MB, 提交时间: 2024-10-22 09:25:34

// 分类讨论
func constructGridLayout(n int, edges [][]int) [][]int {
    g := make([][]int, n)
    for _, e := range edges {
        x, y := e[0], e[1]
        g[x] = append(g[x], y)
        g[y] = append(g[y], x)
    }

    // 每种度数选一个点
    degToNode := [5]int{-1, -1, -1, -1, -1}
    for x, to := range g {
        degToNode[len(to)] = x
    }

    var row []int
    if degToNode[1] != -1 {
        // 答案只有一列
        row = []int{degToNode[1]}
    } else if degToNode[4] == -1 {
        // 答案只有两列
        x := degToNode[2]
        for _, y := range g[x] {
            if len(g[y]) == 2 {
                row = []int{x, y}
                break
            }
        }
    } else {
        // 答案至少有三列
        // 寻找度数为 2333...32 的序列作为第一排
        x := degToNode[2]
        row = []int{x}
        pre := x
        x = g[x][0]
        for len(g[x]) == 3 {
            row = append(row, x)
            for _, y := range g[x] {
                if y != pre && len(g[y]) < 4 {
                    pre = x
                    x = y
                    break
                }
            }
        }
        row = append(row, x) // x 的度数是 2
    }

    k := len(row)
    ans := make([][]int, n/k)
    ans[0] = row
    vis := make([]bool, n)
    for _, x := range row {
        vis[x] = true
    }
    for i := 1; i < len(ans); i++ {
        ans[i] = make([]int, k)
        for j, x := range ans[i-1] {
            for _, y := range g[x] {
                // x 上左右的邻居都访问过了，没访问过的邻居只会在 x 下面
                if !vis[y] {
                    vis[y] = true
                    ans[i][j] = y
                    break
                }
            }
        }
    }
    return ans
}

// 合三为一
func constructGridLayout2(n int, edges [][]int) [][]int {
	g := make([][]int, n)
	for _, e := range edges {
		x, y := e[0], e[1]
		g[x] = append(g[x], y)
		g[y] = append(g[y], x)
	}

	// 找一个度数最小的点
	x := 0
	for i, to := range g {
		if len(to) < len(g[x]) {
			x = i
		}
	}

	row := []int{x}
	vis := make([]bool, n)
	vis[x] = true
	degSt := len(g[x]) // 起点的度数
	for { // 注意题目保证 n >= 2，可以至少循环一次
		nxt := -1
		for _, y := range g[x] {
			if !vis[y] && (nxt < 0 || len(g[y]) < len(g[nxt])) {
				nxt = y
			}
		}
		x = nxt
		row = append(row, x)
		vis[x] = true
		if len(g[x]) == degSt {
			break
		}
	}

	k := len(row)
	ans := make([][]int, n/k)
	ans[0] = row
	for i := 1; i < len(ans); i++ {
		ans[i] = make([]int, k)
		for j, x := range ans[i-1] {
			for _, y := range g[x] {
				// 上左右的邻居都访问过了，没访问过的邻居只会在 x 下面
				if !vis[y] {
					vis[y] = true
					ans[i][j] = y
					break
				}
			}
		}
	}
	return ans
}