php 解法, 执行用时: 476 ms, 内存消耗: 30.4 MB, 提交时间: 2023-10-10 15:04:10
class Solution {
/**
* @param Integer[][] $grid
* @return Boolean
*/
// 对每个格子的数字判断下一步的方向,以及下一步里的格子能不能联通当前格子。
function hasValidPath($grid) {
$row = count($grid);
$col = count($grid[0]);
$queue = new \SplQueue();
$queue->enqueue([0, 0]);
if ($grid[$row - 1][$col - 1] == 4) {
return false;
}
//数字对应的下一步的格子方向以及下一步应该合理的格子数是哪些。
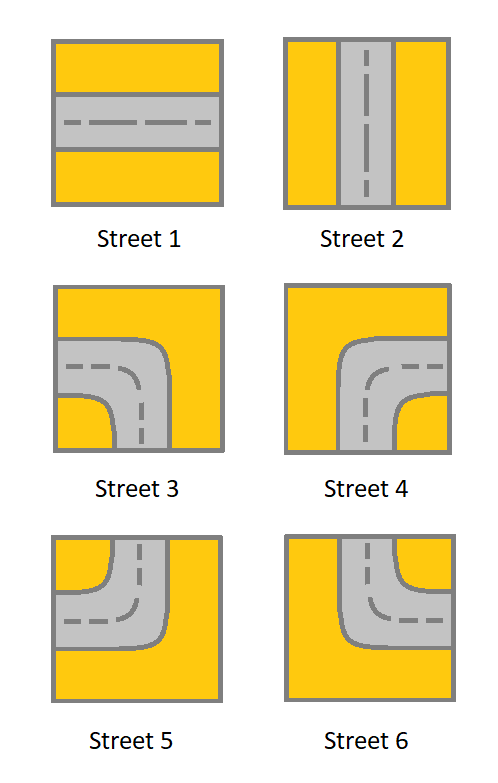
//比如1号数字王右边走的时候,右边的格子只能是,1,5,3号格子。其他格子路不通。
$directions = [
1 => [[0, 1, [3,5,1]], [0, -1, [4,6,1]]],
2 => [[1, 0, [2,5,6]], [-1, 0, [2,3,4]]],
3 => [[0, -1, [1,4,6]], [1, 0, [2,5,6]]],
4 => [[0, 1, [1,3,5]], [1, 0,[2,6,5]]],
5 => [[0, -1, [1,6,4]], [-1, 0, [2,3,4]]],
6 => [[0, 1,[5,3,1]], [-1, 0,[4,3,2]]],
];
$used = array_fill(0, $row, array_fill(0, $col, 0));
while (!$queue->isEmpty()) {
$size = count($queue);
for ($i = 0; $i < $size; $i++) {
$top = $queue->dequeue();
$r = $top[0];
$c = $top[1];
if ($r == $row - 1 && $c == $col - 1) {
return true;
}
$cur = $grid[$r][$c];
foreach ($directions[$cur] as $direction) {
$curValidD = $direction[2];
$newX = $direction[0] + $r;
$newY = $direction[1] + $c;
if ($this->inArea($grid, $newX, $newY) &&
$used[$newX][$newY] == 0 &&
in_array($grid[$newX][$newY], $curValidD)
) {
$used[$newX][$newY] = 1;
$queue->enqueue([$newX, $newY]);
}
}
}
}
return false;
}
function inArea($grid, $i, $j) {
$row = count($grid);
$col = count($grid[0]);
if ($i >=0 && $i < $row && $j >= 0 && $j < $col)
return true;
return false;
}
}
golang 解法, 执行用时: 188 ms, 内存消耗: 67.3 MB, 提交时间: 2023-10-10 15:02:02
func hasValidPath(grid [][]int) bool {
m, n := len(grid)*3, len(grid[0])*3
newGrid := make([][]bool, m)
for i := range newGrid {
newGrid[i] = make([]bool, n)
}
for i := range grid {
for j := range grid[i] {
x, y := 3*j, 3*i
newGrid[y+1][x+1] = true
switch grid[i][j] {
case 1:
newGrid[y+1][x] = true
newGrid[y+1][x+2] = true
case 2:
newGrid[y][x+1] = true
newGrid[y+2][x+1] = true
case 3:
newGrid[y+1][x] = true
newGrid[y+2][x+1] = true
case 4:
newGrid[y+1][x+2] = true
newGrid[y+2][x+1] = true
case 5:
newGrid[y+1][x] = true
newGrid[y][x+1] = true
case 6:
newGrid[y][x+1] = true
newGrid[y+1][x+2] = true
}
}
}
return dfs(1, 1, m, n, newGrid) // 注意起点
}
func dfs(i, j, m, n int, grid [][]bool) bool {
if i == m-1 && j == n-2 { // 终点
return true
}
if i < 0 || i >= m || j < 0 || j >= n || !grid[i][j] {
return false
}
grid[i][j] = false
return dfs(i-1, j, m, n, grid) || dfs(i, j-1, m, n, grid) ||
dfs(i+1, j, m, n, grid) || dfs(i, j+1, m, n, grid)
}
cpp 解法, 执行用时: 160 ms, 内存消耗: 48 MB, 提交时间: 2023-10-10 14:59:44
class Solution {
public:
static constexpr int MAX_N = 300 * 300 + 5;
static constexpr int patterns[7] = {0, 0b1010, 0b0101, 0b1100, 0b0110, 0b1001, 0b0011};
static constexpr int dirs[4][2] = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
struct DisjointSet {
int f[MAX_N];
DisjointSet() {
for (int i = 0; i < MAX_N; ++i) f[i] = i;
}
int find(int x) {
return x == f[x] ? x : f[x] = find(f[x]);
}
void merge(int x, int y) {
f[find(x)] = find(y);
}
} ds;
bool hasValidPath(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
auto getId = [&] (int x, int y) {
return x * n + y;
};
auto handler = [&] (int x, int y) {
int pattern = patterns[grid[x][y]];
for (int i = 0; i < 4; ++i) {
if (pattern & (1 << i)) {
int sx = x + dirs[i][0];
int sy = y + dirs[i][1];
if (sx >= 0 && sx < m && sy >= 0 && sy < n and (patterns[grid[sx][sy]] & (1 << ((i + 2) % 4)))) {
ds.merge(getId(x, y), getId(sx, sy));
}
}
}
};
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
handler(i, j);
}
}
return ds.find(getId(0, 0)) == ds.find(getId(m - 1, n - 1));
}
};
cpp 解法, 执行用时: 248 ms, 内存消耗: 48.8 MB, 提交时间: 2023-10-10 14:59:35
class Solution {
public:
static constexpr int MAX_N = 300 * 300 + 5;
struct DisjointSet {
int f[MAX_N];
DisjointSet() {
for (int i = 0; i < MAX_N; ++i) {
f[i] = i;
}
}
int find(int x) {
return x == f[x] ? x : f[x] = find(f[x]);
}
void merge(int x, int y) {
f[find(x)] = find(y);
}
} ds;
bool hasValidPath(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
auto getId = [&] (int x, int y) {
return x * n + y;
};
auto detectL = [&] (int x, int y) {
if (y - 1 >= 0 && (grid[x][y - 1] == 4 || grid[x][y - 1] == 6 || grid[x][y - 1] == 1)) {
ds.merge(getId(x, y), getId(x, y - 1));
}
};
auto detectR = [&] (int x, int y) {
if (y + 1 < n && (grid[x][y + 1] == 3 || grid[x][y + 1] == 5 || grid[x][y + 1] == 1)) {
ds.merge(getId(x, y), getId(x, y + 1));
}
};
auto detectU = [&] (int x, int y) {
if (x - 1 >= 0 && (grid[x - 1][y] == 3 || grid[x - 1][y] == 4 || grid[x - 1][y] == 2)) {
ds.merge(getId(x, y), getId(x - 1, y));
}
};
auto detectD = [&] (int x, int y) {
if (x + 1 < m && (grid[x + 1][y] == 5 || grid[x + 1][y] == 6 || grid[x + 1][y] == 2)) {
ds.merge(getId(x, y), getId(x + 1, y));
}
};
auto handler = [&] (int x, int y) {
switch (grid[x][y]) {
case 1: {
detectL(x, y); detectR(x, y);
} break;
case 2: {
detectU(x, y); detectD(x, y);
} break;
case 3: {
detectL(x, y); detectD(x, y);
} break;
case 4: {
detectR(x, y); detectD(x, y);
} break;
case 5: {
detectL(x, y); detectU(x, y);
} break;
case 6: {
detectR(x, y); detectU(x, y);
}
}
};
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
handler(i, j);
}
}
return ds.find(getId(0, 0)) == ds.find(getId(m - 1, n - 1));
}
};
java 解法, 执行用时: 37 ms, 内存消耗: 55.9 MB, 提交时间: 2023-10-10 14:59:16
class Solution {
class DisjointSet {
int[] f;
public DisjointSet(int m, int n) {
f = new int[m * n];
for (int i = 0; i < m * n; ++i) {
f[i] = i;
}
}
public int find(int x) {
return x == f[x] ? x : (f[x] = find(f[x]));
}
public void merge(int x, int y) {
f[find(x)] = find(y);
}
}
int[][] grid;
int m, n;
DisjointSet ds;
public boolean hasValidPath(int[][] grid) {
this.grid = grid;
m = grid.length;
n = grid[0].length;
ds = new DisjointSet(m, n);
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
handler(i, j);
}
}
return ds.find(getId(0, 0)) == ds.find(getId(m - 1, n - 1));
}
public int getId(int x, int y) {
return x * n + y;
}
public void detectL(int x, int y) {
if (y - 1 >= 0 && (grid[x][y - 1] == 4 || grid[x][y - 1] == 6 || grid[x][y - 1] == 1)) {
ds.merge(getId(x, y), getId(x, y - 1));
}
}
public void detectR(int x, int y) {
if (y + 1 < n && (grid[x][y + 1] == 3 || grid[x][y + 1] == 5 || grid[x][y + 1] == 1)) {
ds.merge(getId(x, y), getId(x, y + 1));
}
}
public void detectU(int x, int y) {
if (x - 1 >= 0 && (grid[x - 1][y] == 3 || grid[x - 1][y] == 4 || grid[x - 1][y] == 2)) {
ds.merge(getId(x, y), getId(x - 1, y));
}
}
public void detectD(int x, int y) {
if (x + 1 < m && (grid[x + 1][y] == 5 || grid[x + 1][y] == 6 || grid[x + 1][y] == 2)) {
ds.merge(getId(x, y), getId(x + 1, y));
}
}
public void handler(int x, int y) {
switch (grid[x][y]) {
case 1:
detectL(x, y);
detectR(x, y);
break;
case 2:
detectU(x, y);
detectD(x, y);
break;
case 3:
detectL(x, y);
detectD(x, y);
break;
case 4:
detectR(x, y);
detectD(x, y);
break;
case 5:
detectL(x, y);
detectU(x, y);
break;
case 6:
detectR(x, y);
detectU(x, y);
}
}
}
java 解法, 执行用时: 53 ms, 内存消耗: 54.4 MB, 提交时间: 2023-10-10 14:59:03
class Solution {
class DisjointSet {
int[] f;
public DisjointSet(int m, int n) {
f = new int[m * n];
for (int i = 0; i < m * n; ++i) {
f[i] = i;
}
}
public int find(int x) {
return x == f[x] ? x : (f[x] = find(f[x]));
}
public void merge(int x, int y) {
f[find(x)] = find(y);
}
}
int[] patterns = {0, 0b1010, 0b0101, 0b1100, 0b0110, 0b1001, 0b0011};
int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
int[][] grid;
int m, n;
DisjointSet ds;
public boolean hasValidPath(int[][] grid) {
this.grid = grid;
m = grid.length;
n = grid[0].length;
ds = new DisjointSet(m, n);
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
handler(i, j);
}
}
return ds.find(getId(0, 0)) == ds.find(getId(m - 1, n - 1));
}
public int getId(int x, int y) {
return x * n + y;
}
public void handler(int x, int y) {
int pattern = patterns[grid[x][y]];
for (int i = 0; i < 4; ++i) {
if ((pattern & (1 << i)) != 0) {
int sx = x + dirs[i][0];
int sy = y + dirs[i][1];
if (sx >= 0 && sx < m && sy >= 0 && sy < n && (patterns[grid[sx][sy]] & (1 << ((i + 2) % 4))) != 0) {
ds.merge(getId(x, y), getId(sx, sy));
}
}
}
}
}
python3 解法, 执行用时: 2176 ms, 内存消耗: 44.8 MB, 提交时间: 2023-10-10 14:58:39
class Solution:
class DisjointSet:
def __init__(self, n):
self.f = list(range(n))
def find(self, x):
if x == self.f[x]:
return x
self.f[x] = self.find(self.f[x])
return self.f[x]
def merge(self, x, y):
self.f[self.find(x)] = self.find(y)
# 单元格性质建图
def hasValidPath(self, grid: List[List[int]]) -> bool:
m, n = len(grid), len(grid[0])
patterns = [0, 0b1010, 0b0101, 0b1100, 0b0110, 0b1001, 0b0011]
dirs = [(-1, 0), (0, 1), (1, 0), (0, -1)]
ds = Solution.DisjointSet(m * n)
def getId(x, y):
return x * n + y
def handler(x, y):
pattern = patterns[grid[x][y]]
for i, (dx, dy) in enumerate(dirs):
if (pattern & (1 << i)) > 0:
sx, sy = x + dx, y + dy
if 0 <= sx < m and 0 <= sy < n and (patterns[grid[sx][sy]] & (1 << ((i + 2) % 4))) > 0:
ds.merge(getId(x, y), getId(sx, sy))
for i in range(m):
for j in range(n):
handler(i, j)
return ds.find(getId(0, 0)) == ds.find(getId(m - 1, n - 1))
python3 解法, 执行用时: 1540 ms, 内存消耗: 67 MB, 提交时间: 2023-10-10 14:58:04
class Solution:
class DisjointSet:
def __init__(self, n):
self.f = list(range(n))
def find(self, x):
if x == self.f[x]:
return x
self.f[x] = self.find(self.f[x])
return self.f[x]
def merge(self, x, y):
self.f[self.find(x)] = self.find(y)
# 邻接关系建图
def hasValidPath(self, grid: List[List[int]]) -> bool:
m, n = len(grid), len(grid[0])
ds = Solution.DisjointSet(m * n)
def getId(x, y):
return x * n + y
def detectL(x, y):
if y - 1 >= 0 and grid[x][y - 1] in [1, 4, 6]:
ds.merge(getId(x, y), getId(x, y - 1))
def detectR(x, y):
if y + 1 < n and grid[x][y + 1] in [1, 3, 5]:
ds.merge(getId(x, y), getId(x, y + 1))
def detectU(x, y):
if x - 1 >= 0 and grid[x - 1][y] in [2, 3, 4]:
ds.merge(getId(x, y), getId(x - 1, y))
def detectD(x, y):
if x + 1 < m and grid[x + 1][y] in [2, 5, 6]:
ds.merge(getId(x, y), getId(x + 1, y))
def handler(x, y):
if grid[x][y] == 1:
detectL(x, y)
detectR(x, y)
elif grid[x][y] == 2:
detectU(x, y)
detectD(x, y)
elif grid[x][y] == 3:
detectL(x, y)
detectD(x, y)
elif grid[x][y] == 4:
detectR(x, y)
detectD(x, y)
elif grid[x][y] == 5:
detectL(x, y)
detectU(x, y)
else:
detectR(x, y)
detectU(x, y)
for i in range(m):
for j in range(n):
handler(i, j)
return ds.find(getId(0, 0)) == ds.find(getId(m - 1, n - 1))
cpp 解法, 执行用时: 192 ms, 内存消耗: 67.7 MB, 提交时间: 2023-10-10 14:55:51
// 把每个格子转化成3*3的格子,有道路的地方写上1,之后dfs即可
class Solution {
int map[1000][1000];
void fill(int i, int j, int s) {
map[i+1][j+1]=1;
if(s==1) map[i+1][j]=map[i+1][j+2]=1;
if(s==2) map[i][j+1]=map[i+2][j+1]=1;
if(s==3) map[i+1][j]=map[i+2][j+1]=1;
if(s==4) map[i+1][j+2]=map[i+2][j+1]=1;
if(s==5) map[i+1][j]=map[i][j+1]=1;
if(s==6) map[i+1][j+2]=map[i][j+1]=1;
}
int dir[4][2] = {0,1,1,0,-1,0,0,-1};
void dfs(int x, int y) {
map[x][y]=0;
for(int i=0;i<4;i++) {
int xx = x+dir[i][0];
int yy = y+dir[i][1];
if(map[xx][yy]==0) continue;
dfs(xx, yy);
}
}
public:
bool hasValidPath(vector<vector<int>>& grid) {
memset(map,0,sizeof map);
int n = grid.size();
int m = grid[0].size();
for(int i=1;i<=3*n;i+=3)
for(int j=1;j<=3*m;j+=3)
fill(i,j,grid[i/3][j/3]);
dfs(2,2);
return map[3*n-1][3*m-1]==0;
}
};
cpp 解法, 执行用时: 116 ms, 内存消耗: 47.2 MB, 提交时间: 2023-10-10 14:54:43
/**
* 通过构建pipe数组,将每个拼图转化为四个方向上的移动限制图。
* 例:
* pipe[3][2]=3,代表3号拼图可以由向上的方向进入其中,并转向左方向继续前进。
* pipe[5][3]=-1,代表5号拼图不可以由向左的方向进入其中。
* 其中0代表向下、1代表向右、2代表向上、3代表向左、-1代表不可走
* 这之后问题就变成了一个简单的DFS了
*/
class Solution {
int m,n,dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};//0下、1右、2上、3左
int pipe[7][4]={
{-1,-1,-1,-1},
{-1,1,-1,3},
{0,-1,2,-1},
{-1,0,3,-1},
{-1,-1,1,0},
{3,2,-1,-1},
{1,-1,-1,2}
};
//记录各个拼图块路径的方向,0、1、2、3代表方向,-1代表不可走。
bool vis[302][302];
bool dfs(int x,int y,int dir,vector<vector<int>>& grid){//(x,y,当前方向,地图)
vis[x][y]=1;
if(x==m-1&&y==n-1) return 1;//到达终点
int xx=x+dx[dir];
int yy=y+dy[dir];//得到下一个准备走的坐标
if(xx<0||yy<0||xx>=m||yy>=n)return 0;//越界
int nxt=grid[xx][yy];//得到下一块拼图的编号
if(pipe[nxt][dir]!=-1&&!vis[xx][yy])
return dfs(xx,yy,pipe[nxt][dir],grid);//如果当前方向可走,则方向改变,继续走。
return 0;//无法走,返回0
}
public:
bool hasValidPath(vector<vector<int>>& grid) {
m=grid.size();
n=grid[0].size();
memset(vis,0,sizeof(vis));
int sta=grid[0][0];//起点的拼图编号
for(int i=0;i<4;++i)//朝着四个方向都试一下
if(pipe[sta][i]!=-1)//当前方向可以走
if(dfs(0,0,pipe[sta][i],grid))//沿着当前方向搜索
return 1;//拼图都有两个方向可以走,只要沿着一个初始方向走通就可以。
return 0;
}
};