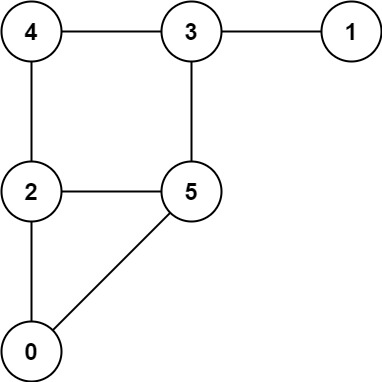
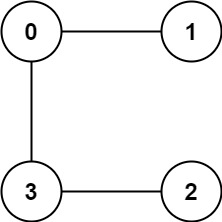
C++
Java
Python
Python3
C
C#
JavaScript
Ruby
Swift
Go
Scala
Kotlin
Rust
PHP
TypeScript
Racket
Erlang
Elixir
Dart
monokai
ambiance
chaos
chrome
cloud9_day
cloud9_night
cloud9_night_low_color
clouds
clouds_midnight
cobalt
crimson_editor
dawn
dracula
dreamweaver
eclipse
github
github_dark
gob
gruvbox
gruvbox_dark_hard
gruvbox_light_hard
idle_fingers
iplastic
katzenmilch
kr_theme
kuroir
merbivore
merbivore_soft
mono_industrial
nord_dark
one_dark
pastel_on_dark
solarized_dark
solarized_light
sqlserver
terminal
textmate
tomorrow
tomorrow_night
tomorrow_night_blue
tomorrow_night_bright
tomorrow_night_eighties
twilight
vibrant_ink
xcode
上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
int catMouseGame(vector<vector<int>>& graph) {
}
};
运行代码
提交
javascript 解法, 执行用时: 247 ms, 内存消耗: 66.3 MB, 提交时间: 2025-02-10 09:25:48
/**
* @param {number[][]} graph
* @return {number}
*/
const MOUSE_TURN = 0, CAT_TURN = 1;
const DRAW = 0, MOUSE_WIN = 1, CAT_WIN = 2;
var catMouseGame = function(graph) {
const n = graph.length;
degrees = new Array(n).fill(0).map(() => new Array(n).fill(0).map(() => new Array(2).fill(0)));
results = new Array(n).fill(0).map(() => new Array(n).fill(0).map(() => new Array(2).fill(0)));
const queue = [];
for (let i = 0; i < n; i++) {
for (let j = 1; j < n; j++) {
degrees[i][j][MOUSE_TURN] = graph[i].length;
degrees[i][j][CAT_TURN] = graph[j].length;
}
}
for (const node of graph[0]) {
for (let i = 0; i < n; i++) {
degrees[i][node][CAT_TURN]--;
}
}
for (let j = 1; j < n; j++) {
results[0][j][MOUSE_TURN] = MOUSE_WIN;
results[0][j][CAT_TURN] = MOUSE_WIN;
queue.push([0, j, MOUSE_TURN]);
queue.push([0, j, CAT_TURN]);
}
for (let i = 1; i < n; i++) {
results[i][i][MOUSE_TURN] = CAT_WIN;
results[i][i][CAT_TURN] = CAT_WIN;
queue.push([i, i, MOUSE_TURN]);
queue.push([i, i, CAT_TURN]);
}
while (queue.length) {
const state = queue.shift();
const mouse = state[0], cat = state[1], turn = state[2];
const result = results[mouse][cat][turn];
const prevStates = getPrevStates(mouse, cat, turn, graph);
for (const prevState of prevStates) {
let prevMouse = prevState[0], prevCat = prevState[1], prevTurn = prevState[2];
if (results[prevMouse][prevCat][prevTurn] === DRAW) {
const canWin = (result === MOUSE_WIN && prevTurn === MOUSE_TURN) || (result === CAT_WIN && prevTurn === CAT_TURN);
if (canWin) {
results[prevMouse][prevCat][prevTurn] = result;
queue.push([prevMouse, prevCat, prevTurn]);
} else {
degrees[prevMouse][prevCat][prevTurn]--;
if (degrees[prevMouse][prevCat][prevTurn] == 0) {
const loseResult = prevTurn === MOUSE_TURN ? CAT_WIN : MOUSE_WIN;
results[prevMouse][prevCat][prevTurn] = loseResult;
queue.push([prevMouse, prevCat, prevTurn]);
}
}
}
}
}
return results[1][2][MOUSE_TURN];
};
const getPrevStates = (mouse, cat, turn, graph) => {
const prevStates = [];
const prevTurn = turn == MOUSE_TURN ? CAT_TURN : MOUSE_TURN;
if (prevTurn === MOUSE_TURN) {
for (const prev of graph[mouse]) {
prevStates.push([prev, cat, prevTurn]);
}
} else {
for (const prev of graph[cat]) {
if (prev != 0) {
prevStates.push([mouse, prev, prevTurn]);
}
}
}
return prevStates;
}
cpp 解法, 执行用时: 211 ms, 内存消耗: 107.8 MB, 提交时间: 2025-02-10 09:25:12
class Solution {
public:
const int MOUSE_TURN = 0, CAT_TURN = 1;
const int DRAW = 0, MOUSE_WIN = 1, CAT_WIN = 2;
vector<vector<int>> graph;
vector<vector<vector<int>>> degrees;
vector<vector<vector<int>>> results;
int catMouseGame(vector<vector<int>>& graph) {
int n = graph.size();
this->graph = graph;
this->degrees = vector<vector<vector<int>>>(n, vector<vector<int>>(n, vector<int>(2)));
this->results = vector<vector<vector<int>>>(n, vector<vector<int>>(n, vector<int>(2)));
queue<tuple<int, int, int>> qu;
for (int i = 0; i < n; i++) {
for (int j = 1; j < n; j++) {
degrees[i][j][MOUSE_TURN] = graph[i].size();
degrees[i][j][CAT_TURN] = graph[j].size();
}
}
for (int node : graph[0]) {
for (int i = 0; i < n; i++) {
degrees[i][node][CAT_TURN]--;
}
}
for (int j = 1; j < n; j++) {
results[0][j][MOUSE_TURN] = MOUSE_WIN;
results[0][j][CAT_TURN] = MOUSE_WIN;
qu.emplace(0, j, MOUSE_TURN);
qu.emplace(0, j, CAT_TURN);
}
for (int i = 1; i < n; i++) {
results[i][i][MOUSE_TURN] = CAT_WIN;
results[i][i][CAT_TURN] = CAT_WIN;
qu.emplace(i, i, MOUSE_TURN);
qu.emplace(i, i, CAT_TURN);
}
while (!qu.empty()) {
auto [mouse, cat, turn] = qu.front();
qu.pop();
int result = results[mouse][cat][turn];
vector<tuple<int, int, int>> prevStates = GetPrevStates(mouse, cat, turn);
for (auto & [prevMouse, prevCat, prevTurn] : prevStates) {
if (results[prevMouse][prevCat][prevTurn] == DRAW) {
bool canWin = (result == MOUSE_WIN && prevTurn == MOUSE_TURN) || (result == CAT_WIN && prevTurn == CAT_TURN);
if (canWin) {
results[prevMouse][prevCat][prevTurn] = result;
qu.emplace(prevMouse, prevCat, prevTurn);
} else if (--degrees[prevMouse][prevCat][prevTurn] == 0) {
int loseResult = prevTurn == MOUSE_TURN ? CAT_WIN : MOUSE_WIN;
results[prevMouse][prevCat][prevTurn] = loseResult;
qu.emplace(prevMouse, prevCat, prevTurn);
}
}
}
}
return results[1][2][MOUSE_TURN];
}
vector<tuple<int, int, int>> GetPrevStates(int mouse, int cat, int turn) {
vector<tuple<int, int, int>> prevStates;
int prevTurn = turn == MOUSE_TURN ? CAT_TURN : MOUSE_TURN;
if (prevTurn == MOUSE_TURN) {
for (int & prev : graph[mouse]) {
prevStates.emplace_back(prev, cat, prevTurn);
}
} else {
for (int & prev : graph[cat]) {
if (prev != 0) {
prevStates.emplace_back(mouse, prev, prevTurn);
}
}
}
return prevStates;
}
};
golang 解法, 执行用时: 44 ms, 内存消耗: 7.5 MB, 提交时间: 2023-10-25 11:27:32
const (
mouseTurn = 0
catTurn = 1
draw = 0
mouseWin = 1
catWin = 2
)
func catMouseGame(graph [][]int) int {
n := len(graph)
degrees := make([][][2]int, n)
results := make([][][2]int, n)
for i := range degrees {
degrees[i] = make([][2]int, n)
results[i] = make([][2]int, n)
}
for i, to := range graph {
for j := 1; j < n; j++ {
degrees[i][j][mouseTurn] = len(to)
degrees[i][j][catTurn] = len(graph[j])
}
}
for _, y := range graph[0] {
for i := range degrees {
degrees[i][y][catTurn]--
}
}
type state struct{ mouse, cat, turn int }
q := []state{}
for j := 1; j < n; j++ {
results[0][j][mouseTurn] = mouseWin
results[0][j][catTurn] = mouseWin
q = append(q, state{0, j, mouseTurn}, state{0, j, catTurn})
}
for i := 1; i < n; i++ {
results[i][i][mouseTurn] = catWin
results[i][i][catTurn] = catWin
q = append(q, state{i, i, mouseTurn}, state{i, i, catTurn})
}
getPrevStates := func(s state) (prevStates []state) {
if s.turn == mouseTurn {
for _, prev := range graph[s.cat] {
if prev != 0 {
prevStates = append(prevStates, state{s.mouse, prev, catTurn})
}
}
} else {
for _, prev := range graph[s.mouse] {
prevStates = append(prevStates, state{prev, s.cat, mouseTurn})
}
}
return
}
for len(q) > 0 {
s := q[0]
q = q[1:]
result := results[s.mouse][s.cat][s.turn]
for _, p := range getPrevStates(s) {
prevMouse, prevCat, prevTurn := p.mouse, p.cat, p.turn
if results[prevMouse][prevCat][prevTurn] == draw {
canWin := result == mouseWin && prevTurn == mouseTurn || result == catWin && prevTurn == catTurn
if canWin {
results[prevMouse][prevCat][prevTurn] = result
q = append(q, p)
} else {
degrees[prevMouse][prevCat][prevTurn]--
if degrees[prevMouse][prevCat][prevTurn] == 0 {
if prevTurn == mouseTurn {
results[prevMouse][prevCat][prevTurn] = catWin
} else {
results[prevMouse][prevCat][prevTurn] = mouseWin
}
q = append(q, p)
}
}
}
}
}
return results[1][2][mouseTurn]
}
python3 解法, 执行用时: 564 ms, 内存消耗: 16.8 MB, 提交时间: 2023-10-25 11:27:18
MOUSE_TURN = 0
CAT_TURN = 1
DRAW = 0
MOUSE_WIN = 1
CAT_WIN = 2
class Solution:
def catMouseGame(self, graph: List[List[int]]) -> int:
n = len(graph)
degrees = [[[0, 0] for _ in range(n)] for _ in range(n)]
results = [[[0, 0] for _ in range(n)] for _ in range(n)]
for i in range(n):
for j in range(1, n):
degrees[i][j][MOUSE_TURN] = len(graph[i])
degrees[i][j][CAT_TURN] = len(graph[j])
for y in graph[0]:
for i in range(n):
degrees[i][y][CAT_TURN] -= 1
q = deque()
for j in range(1, n):
results[0][j][MOUSE_TURN] = MOUSE_WIN
results[0][j][CAT_TURN] = MOUSE_WIN
q.append((0, j, MOUSE_TURN))
q.append((0, j, CAT_TURN))
for i in range(1, n):
results[i][i][MOUSE_TURN] = CAT_WIN
results[i][i][CAT_TURN] = CAT_WIN
q.append((i, i, MOUSE_TURN))
q.append((i, i, CAT_TURN))
while q:
mouse, cat, turn = q.popleft()
result = results[mouse][cat][turn]
if turn == MOUSE_TURN:
prevStates = [(mouse, prev, CAT_TURN) for prev in graph[cat]]
else:
prevStates = [(prev, cat, MOUSE_TURN) for prev in graph[mouse]]
for prevMouse, prevCat, prevTurn in prevStates:
if prevCat == 0:
continue
if results[prevMouse][prevCat][prevTurn] == DRAW:
canWin = result == MOUSE_WIN and prevTurn == MOUSE_TURN or result == CAT_WIN and prevTurn == CAT_TURN
if canWin:
results[prevMouse][prevCat][prevTurn] = result
q.append((prevMouse, prevCat, prevTurn))
else:
degrees[prevMouse][prevCat][prevTurn] -= 1
if degrees[prevMouse][prevCat][prevTurn] == 0:
results[prevMouse][prevCat][prevTurn] = CAT_WIN if prevTurn == MOUSE_TURN else MOUSE_WIN
q.append((prevMouse, prevCat, prevTurn))
return results[1][2][MOUSE_TURN]
java 解法, 执行用时: 58 ms, 内存消耗: 43 MB, 提交时间: 2023-10-25 11:27:02
class Solution {
static final int MOUSE_TURN = 0, CAT_TURN = 1;
static final int DRAW = 0, MOUSE_WIN = 1, CAT_WIN = 2;
int[][] graph;
int[][][] degrees;
int[][][] results;
public int catMouseGame(int[][] graph) {
int n = graph.length;
this.graph = graph;
this.degrees = new int[n][n][2];
this.results = new int[n][n][2];
Queue<int[]> queue = new ArrayDeque<int[]>();
for (int i = 0; i < n; i++) {
for (int j = 1; j < n; j++) {
degrees[i][j][MOUSE_TURN] = graph[i].length;
degrees[i][j][CAT_TURN] = graph[j].length;
}
}
for (int node : graph[0]) {
for (int i = 0; i < n; i++) {
degrees[i][node][CAT_TURN]--;
}
}
for (int j = 1; j < n; j++) {
results[0][j][MOUSE_TURN] = MOUSE_WIN;
results[0][j][CAT_TURN] = MOUSE_WIN;
queue.offer(new int[]{0, j, MOUSE_TURN});
queue.offer(new int[]{0, j, CAT_TURN});
}
for (int i = 1; i < n; i++) {
results[i][i][MOUSE_TURN] = CAT_WIN;
results[i][i][CAT_TURN] = CAT_WIN;
queue.offer(new int[]{i, i, MOUSE_TURN});
queue.offer(new int[]{i, i, CAT_TURN});
}
while (!queue.isEmpty()) {
int[] state = queue.poll();
int mouse = state[0], cat = state[1], turn = state[2];
int result = results[mouse][cat][turn];
List<int[]> prevStates = getPrevStates(mouse, cat, turn);
for (int[] prevState : prevStates) {
int prevMouse = prevState[0], prevCat = prevState[1], prevTurn = prevState[2];
if (results[prevMouse][prevCat][prevTurn] == DRAW) {
boolean canWin = (result == MOUSE_WIN && prevTurn == MOUSE_TURN) || (result == CAT_WIN && prevTurn == CAT_TURN);
if (canWin) {
results[prevMouse][prevCat][prevTurn] = result;
queue.offer(new int[]{prevMouse, prevCat, prevTurn});
} else {
degrees[prevMouse][prevCat][prevTurn]--;
if (degrees[prevMouse][prevCat][prevTurn] == 0) {
int loseResult = prevTurn == MOUSE_TURN ? CAT_WIN : MOUSE_WIN;
results[prevMouse][prevCat][prevTurn] = loseResult;
queue.offer(new int[]{prevMouse, prevCat, prevTurn});
}
}
}
}
}
return results[1][2][MOUSE_TURN];
}
public List<int[]> getPrevStates(int mouse, int cat, int turn) {
List<int[]> prevStates = new ArrayList<int[]>();
int prevTurn = turn == MOUSE_TURN ? CAT_TURN : MOUSE_TURN;
if (prevTurn == MOUSE_TURN) {
for (int prev : graph[mouse]) {
prevStates.add(new int[]{prev, cat, prevTurn});
}
} else {
for (int prev : graph[cat]) {
if (prev != 0) {
prevStates.add(new int[]{mouse, prev, prevTurn});
}
}
}
return prevStates;
}
}