python3 解法, 执行用时: 36 ms, 内存消耗: 16.3 MB, 提交时间: 2023-10-21 22:51:18
# Definition for a binary tree node.
# class Node(object):
# def __init__(self, val=" ", left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def expTree(self, s: str) -> 'Node':
priority = {"(":0, "*":1, "/":1, "+":2, "-":2}
nums, opts = [], []
cur = 0
while cur < len(s):
#所有入栈的元素都是节点
if s[cur].isnumeric(): #数字直接入栈
temp = cur
while cur < len(s) and s[cur].isnumeric():
cur += 1
nums.append(Node(val = s[temp:cur]))
continue
elif s[cur] == '(': #左括号直接入栈
opts.append(Node(val = "("))
elif s[cur] == ')': #把括号内的全部算完
while len(opts) > 0 and priority[opts[-1].val] > 0:
y, x, opt = nums.pop(), nums.pop(), opts.pop()
opt.left, opt.right = x, y
nums.append(opt)
opts.pop() #去掉左括号
else:
#把上一个左括号前优先级比自己大或等于自己的算完
while len(opts) > 0 and opts[-1].val != '(' and priority[opts[-1].val] <= priority[s[cur]]:
y, x, opt = nums.pop(), nums.pop(), opts.pop()
opt.left, opt.right = x, y
nums.append(opt)
opts.append(Node(val = s[cur]))
cur += 1
#按序处理剩下的
while len(opts) > 0:
y, x, opt = nums.pop(), nums.pop(), opts.pop()
opt.left, opt.right = x, y
nums.append(opt)
return nums[0]
cpp 解法, 执行用时: 4 ms, 内存消耗: 7.1 MB, 提交时间: 2023-10-21 22:50:52
/**
* Definition for a binary tree node.
* struct Node {
* char val;
* Node *left;
* Node *right;
* Node() : val(' '), left(nullptr), right(nullptr) {}
* Node(char x) : val(x), left(nullptr), right(nullptr) {}
* Node(char x, Node *left, Node *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
// 按照需求构建的stack
stack<Node*> nums;
// 从低到顶优先级递增的stack
stack<char> ops;
// 优先级数字越大,计算优先级越高
int Priority(char& c) {
if (c == '(') {
return 4;
} else if (c == '*' || c == '/') {
return 3;
} else if (c == '+' || c == '-') {
return 2;
} else {
return 1;
}
}
// 弹出上一个op作为根节点,然后弹出连个nums左右左右节点
void PopOps() {
// cout << "PopOps" << endl;
// 先弹的是right
Node* right = nums.top();
nums.pop();
// 后滩的是left
Node* left = nums.top();
nums.pop();
// cout << "pop " << ops.top() << " with " << left->val << " " << right->val << endl;
Node* root = new Node(ops.top(), left, right);
ops.pop();
nums.push(root);
}
public:
Node* expTree(string s) {
for (char c : s) {
// cout << c << endl;
// 题目假设数字就是一位
if (c >= '0' && c <= '9') {
nums.push(new Node(c));
} else {
// 空或者当前优先级更高时候直接插入 ops
if (ops.empty() || Priority(ops.top()) < Priority(c)) {
ops.push(c);
} else {
// 不断弹出优先级更高的直到遇到 ( 为止
while (!ops.empty() && ops.top() != '(' && Priority(ops.top()) >= Priority(c)) {
PopOps();
}
if (c != ')') {
ops.push(c);
} else {
// 忽略 ) 的特殊处理,无需插入),反而要弹出(,其他则插入更高优先级的op
ops.pop();
}
}
}
}
// 把ops栈里清空
while (!ops.empty()) {
PopOps();
}
return nums.top();
}
};
java 解法, 执行用时: 1 ms, 内存消耗: 39.4 MB, 提交时间: 2023-10-21 22:48:39
/**
* Definition for a binary tree node.
* class Node {
* char val;
* Node left;
* Node right;
* Node() {this.val = ' ';}
* Node(char val) { this.val = val; }
* Node(char val, Node left, Node right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
/**
* 利用后缀表达式构造二叉表达式树
*/
public Node expTree(String s) {
s = infixToPostfix(s);
Stack<Node> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
// 先利用当前值构造Node节点
Node tmp = new Node(s.charAt(i));
switch (tmp.val) {
case '+':
case '-':
case '*':
case '/':
// 运算符节点有左右两个儿子,两个儿子通过弹栈获取
tmp.right = stack.pop();
tmp.left = stack.pop();
break;
default:
// 运算数节点没有儿子
}
stack.push(tmp);
}
return stack.pop();
}
/**
* 中缀表达式转换为后缀表达式 "3*4-2*5" -> "34*25-"
* 后缀表达式也就是逆波兰表达式。
*/
private String infixToPostfix(String s) {
Stack<Character> stack = new Stack<>();
StringBuilder sb = new StringBuilder();
for (int i = 0; i < s.length(); i++) {
switch (s.charAt(i)) {
case '+':
case '-':
while(!stack.isEmpty() && stack.peek() != '(')
sb.append(stack.pop());
stack.push(s.charAt(i));
break;
case '*':
case '/':
while(!stack.isEmpty() && stack.peek() != '(' && stack.peek() != '+' && stack.peek() != '-')
sb.append(stack.pop());
stack.push(s.charAt(i));
break;
case '(':
stack.push(s.charAt(i));
break;
case ')':
while(stack.peek() != '(')
sb.append(stack.pop());
stack.pop();
break;
default:
stack.push(s.charAt(i));
}
}
while(!stack.isEmpty())
sb.append(stack.pop());
return sb.toString();
}
}
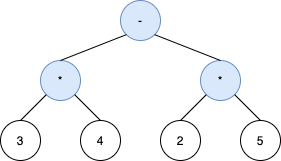
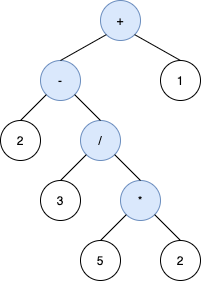
下面的树也是无效的。尽管它的计算结果相等并与上述树等效,但其中序遍历不会产生 s ,并且其操作数与 s 中的顺序也不相同。