2015. 每段建筑物的平均高度

一条完全笔直的街道由一条数字线表示。街道上有建筑物，由二维整数阵列 buildings 表示，其中 buildings[i] = [starti, endi, heighti]。这意味着在 半封闭的位置[starti，endi] 有一座高度为 heighti 的建筑。
你想用 最少 数量的非重叠 部分 来 描述 街道上建筑物的高度。街道可以用2D整数数组 street 来表示，其中 street[j] = [leftj, rightj, averagej] 描述了道路的 半封闭区域 [leftj, rightj) ，该段中建筑物的 平均 高度为 averagej 。

• 例如，如果 buildings = [[1,5,2],[3,10,4]] ， street = [[1,3,2],[3,5,3],[5,10,4]] 可以表示街道，因为：
  • 从 1 到 3 ，只有第一栋建筑的平均高度为 2 / 1 = 2 。
  • 从 3 到 5 ，第一和第二栋建筑的平均高度均为 （2+4） / 2 = 3 。
  • 从 5 到 10 ，只有第二栋建筑的平均高度为 4 / 1 = 4 。

给定 buildings ，返回如上所述的二维整数矩阵 street （ 不包括 街道上没有建筑物的任何区域）。您可以按 任何顺序 返回数组。
n 个元素的 平均值 是 n 个元素除以 n 的 总和 （整数除法）。
半闭合段 [a, b) 是点 a 和 b 之间的数字线的截面，包括 点 a ，不包括 点 b 。

示例1：

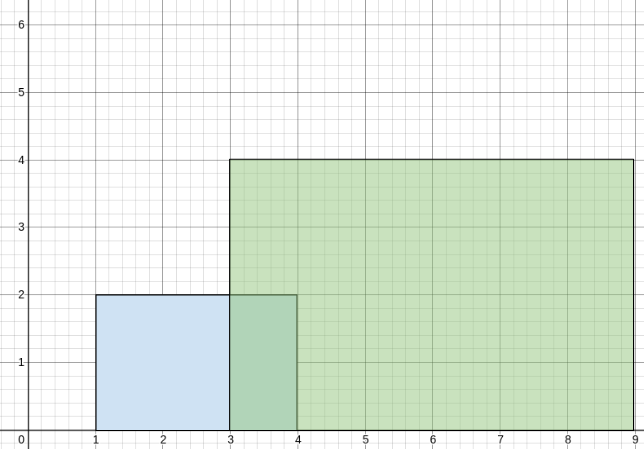
输入: buildings = [[1,4,2],[3,9,4]]
输出: [[1,3,2],[3,4,3],[4,9,4]]
解释:
从 1 到 3 ，只有第一栋建筑的平均高度为 2 / 1 = 2。
从 3 到 4 ，第一和第二栋建筑的平均高度均为（2+4）/ 2 = 3。
从 4 到 9 ，只有第二栋建筑的平均高度为 4 / 1 = 4。

示例 2:

输入: buildings = [[1,3,2],[2,5,3],[2,8,3]]
输出: [[1,3,2],[3,8,3]]
解释:
从 1 到 2 ，只有第一栋建筑的平均高度为 2 / 1 = 2。
从 2 到 3 ，这三座建筑的平均高度均为 （2+3+3） / 3 = 2。
从 3 到 5 ，第二和第三栋楼都在那里，平均高度为 （3+3） / 2 = 3。
从 5 到 8 ，只有最后一栋建筑的平均高度为 3 / 1 = 3。
从 1 到 3 的平均高度是相同的，所以我们可以把它们分成一个部分。
从 3 到 8 的平均高度是相同的，所以我们可以把它们分成一个部分。

示例 3:

输入: buildings = [[1,2,1],[5,6,1]]
输出: [[1,2,1],[5,6,1]]
解释:
从 1 到 2 ，只有第一栋建筑的平均高度为 1 / 1 = 1。
从 2 到 5 ，没有建筑物，因此不包括在输出中。
从 5 到 6 ，只有第二栋建筑的平均高度为 1 / 1 = 1。
我们无法将这些部分组合在一起，因为没有建筑的空白空间将这些部分隔开。

提示:

• 1 <= buildings.length <= 105
• buildings[i].length == 3
• 0 <= starti < endi <= 108
• 1 <= heighti <= 105