cpp 解法, 执行用时: 120 ms, 内存消耗: 8.5 MB, 提交时间: 2023-10-25 22:57:18
class Solution {
public:
int index(char c) {
switch (c) {
case 'E':return 0;
case 'S':return 1;
case 'W':return 2;
case 'N':return 3;
}
return -1;
}
bool check1(int x, int y) {
return ((x == 1 || x == 2) && (y == 1 || y == 2)) || (x == 3 && y == 2);
}
bool check2(int x, int y) {
return (x == 1 && (y == 2 || y == 3)) || ((x == 2 || x == 3) && y == 1);
}
bool check(int s0, int s1, int s2, int s3) {
return check1(s0, s1) || check1(s1, s2) || check1(s2, s3) || check1(s3, s0) || check2(s0, s2) || check2(s1, s3);
}
int trafficCommand(vector<string>& directions) {
const int n0 = directions[0].size();
const int n1 = directions[1].size();
const int n2 = directions[2].size();
const int n3 = directions[3].size();
int dp[n0 + 1][n1 + 1][n2 + 1][n3 + 1];
memset(dp, 0x3f, sizeof(dp));
dp[0][0][0][0] = 0;
for (int i = 0;i <= n0;++i) {
const int d0 = i > 0 ? (index(directions[0][i - 1]) + 0) % 4 : -1;
for (int j = 0;j <= n1;++j) {
const int d1 = j > 0 ? (index(directions[1][j - 1]) + 3) % 4 : -1;
for (int k = 0;k <= n2;++k) {
const int d2 = k > 0 ? (index(directions[2][k - 1]) + 2) % 4 : -1;
for (int l = 0;l <= n3;++l) {
const int d3 = l > 0 ? (index(directions[3][l - 1]) + 1) % 4 : -1;
int ans = dp[i][j][k][l];
for (int p = 1;p < 16;++p) {
const int p0 = p & 1;
const int p1 = p >> 1 & 1;
const int p2 = p >> 2 & 1;
const int p3 = p >> 3 & 1;
if (i < p0 || j < p1 || k < p2 || l < p3) continue;
if (!check(p0 ? d0 : -1, p1 ? d1 : -1, p2 ? d2 : -1, p3 ? d3 : -1))
ans = min(ans, dp[i - p0][j - p1][k - p2][l - p3] + 1);
}
dp[i][j][k][l] = ans;
}
}
}
}
return dp[n0][n1][n2][n3];
}
};
python3 解法, 执行用时: 5724 ms, 内存消耗: 18.2 MB, 提交时间: 2023-10-25 22:56:59
able = set()
def test(a, b, c, d, A, B, C, D): # eswn
if a == C and (b == D or d == A or d == B or c == D):
return False
if a == B and (b == C or b == D or d == A or c == A):
return False
return True
for e in ' WNS':
for s in ' EWN':
for w in ' ESN':
for n in ' ESW':
eswn = e + s + w + n
t = eswn.replace(' ', '')
if not t:
continue
if len(set(t)) != len(t):
continue
if not test(e, s, w, n, *'ESWN'):
continue
if not test(s, w, n, e, *'SWNE'):
continue
if not test(w, n, e, s, *'WNES'):
continue
if not test(n, e, s, w, *'NESW'):
continue
able.add(eswn)
class Solution:
def trafficCommand(self, directions: List[str]) -> int:
[e, s, w, n] = list(map(len, directions))
[ce, cs, cw, cn] = directions
f = [[[[100]*(n+1) for _ in range(w+1)] for _ in range(s+1)] for _ in range(e+1)]
ddd = {}
f[0][0][0][0] = 0
for e1 in range(e+1):
for s1 in range(s+1):
for w1 in range(w+1):
for n1 in range(n+1):
if e1 + s1 + w1 + n1 == 0:
continue
x = 100
for mask in range(1, 16):
v = ce[e1-1] if mask & 1 and e1 else ' '
v += cs[s1-1] if mask & 2 and s1 else ' '
v += cw[w1-1] if mask & 4 and w1 else ' '
v += cn[n1-1] if mask & 8 and n1 else ' '
if v in able:
x = min(x, f[e1-(v[0]!=' ')][s1-(v[1]!=' ')][w1-(v[2]!=' ')][n1-(v[3]!=' ')] + 1)
f[e1][s1][w1][n1] = x
return f[e][s][w][n]
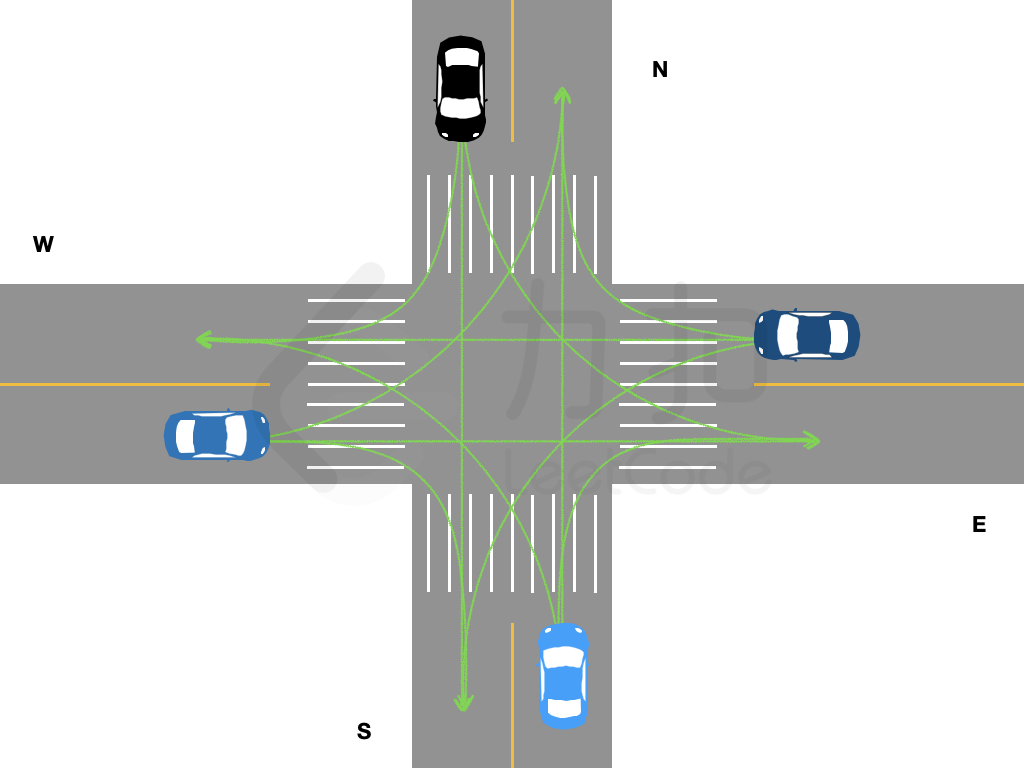 {:height="350px"}
{:height="350px"}